分子分光学の20世紀中の進歩の非常に大きな部分は、この50年ばかりの間に起こったと考えてよい。とくに重要なのは、レーザーが広く普及した70年代の進歩である。筆者が関係したラマン分光学を見てみると、共鳴ラマン、表面増強ラマン散乱 (SERS) 、顕微ラマン、非線形ラマン、時間分解ラマン、ラマン光学活性など今日、非常に注目されている様々なラマン分光法のほとんどが70年代に誕生した1-3。80年代にはFT-IRが広く普及し、顕微赤外、時間分解赤外などが大きく進展した4。 90年代に入ると、まず近赤外分光法が成長し5,6、さらにその後半になるとテラヘルツ分光法（terahertz time-domain spectroscopy; THz-TDS）が登場した7,8。凝集相に関して言えば、20世紀の最後になって紫外域 (190 nm) から遠赤外/テラヘルツ領域 (3.3 cm-1; 0.1THz)までシームレスに繋がったのである1。90年代に入るまでは、レーザーや分光器、検出器などハードの進歩が大方分光学の進歩を引っ張ってきたわけであるが、90年代に入るとソフトの進歩も分光学を支えるようになった。とくに量子化学の発展が目覚ましい9,10。振動分光学、電子分光学など分子分光学のどの分野においても量子化学は中心的な役割を果たしている。

量子化学の分子分光学への応用における最初の非常に重要な出来事は、1964年のK. Kohnらによる密度汎関数法 (Density Functional Theory, DFT) の提案である。DFT法は量子化学計算をかなり高精度で比較的少ない計算リソースで行えるようにした。1970年にはJ. A. PopleらによりGaussian70が発表され、量子化学計算が少し身近なものとなった9,10。90年代に入り、DFT法やソフトが大きく進歩し、振動スペクトルの量子化学計算が活発になった。これらの進歩により普通の有機化合物の振動数の計算がかなりの精度でできるようになった。またいろいろなスケーリングファクター、とくに吉田ら11によるwavenumber linear scaling (WLS) 法の導入により、かなり複雑な分子でない限り、調和振動近似でも、赤外、ラマンスペクトルのシミュレーションができるようになった9,10。非調和性を含む振動解析は、1978年ごろのJ. M. Bowmanら12による振動自己無撞着場(vibrational self-consistent field; VSCF) 法の提案により始まったと考えてよい。2000年代に入って分子振動の非調和性を理論計算するための解析法やプログラムがいろいろと開発された。非調和性を含む計算は一般に膨大な時間とコストを要するが、市販のプログラム・パッケージに組み込まれている非調和性を含む計算法とコンピューターの進歩により、著しい進歩を遂げている9,10,13。

尾崎教授らが最初に量子化学計算を始めたのは、田中丈の加入による。田中丈ら14は2004年、当時としては比較的珍しいSERSスペクトルの解析に量子化学計算を用いた。同年、勝本と田中丈ら15は Poly(N-isopropylacrylamide) 水溶液のコイル―グロビュール転移の研究に赤外分光法とともに量子化学計算を用いた。その後、遠紫外、深紫外、近赤外、赤外、遠赤外/テラヘルツ、ラマン分光に順次量子化学計算の研究を展開した。その流れの中で、尾崎教授らは「分子分光学と量子化学に橋を架ける」ということを目指した。

遠紫外から遠赤外/テラヘルツ、ラマンまで手を広げたわけであるが、（中）赤外、近赤外、遠赤外/テラヘルツ分光法は、基本音、倍音、結合音、分子間振動などいずれも分子の振動を扱うので、振動分光学と考えれば一つの分光学とも考えることができる。広い意味での赤外分光学である。これにラマン分光学を加えて、振動分光学の基礎とその応用の研究に量子化学を用いた。電子分光学としては、遠紫外分光学16-19と近赤外分光学5,6の研究に携わった。近赤外領域には分子振動の倍音、結合音によるバンドのほかに、d-d遷移や電荷移動遷移など電子吸収によるバンドも観測されるので、近赤外分光法は電子分光法でもある。遠紫外から遠赤外/テラヘルツ、ラマンの領域の研究に量子化学を用い、分光学研究における量子化学の重要性を各分野で示すことに努めた。尾崎教授らの研究でとくに力を入れたのは、非調和性を考慮した計算、分子間相互作用を組み入れた計算、高分子のような大きな分子の振動計算である。

ここでは、尾崎研究室で行われた量子化学計算を用いた遠紫外分光法、赤外分光法、近赤外分光法、遠赤外/テラヘルツ/低波数ラマン分光法、ラマン分光の研究を紹介する。

遠紫外域では、π電子のほかσ電子の関係したバンドが観測される （水分子のn-σ*遷移など）。Rydberg遷移によるバンドも観測される16-19。遠紫外域では、溶媒も含めてすべての分子が許容電子遷移を持ち、吸光度が非常に強くなるので (εFUV = 104-106 mol-1 dm3 cm-1）、これまで主に気体を対象として研究が進められてきた16-19。気体の遠紫外スペクトルの測定から、価電子状態やRydberg状態の研究が行われてきた。飽和炭化水素ではσ-Rydberg遷移が、二重結合を持った炭化水素では、π-π*遷移に付随してπ-Rydberg遷移が観測される16-19。凝縮相におけるRydberg遷移については、報告例が非常に少なく、その存在についていろいろと議論があった16。

そこで尾崎教授らは池羽田と東ら中心となり、非常に大きな吸光度の問題を解決するために、赤外分光法でよく用いられているATR法を、2007年に遠紫外域に導入した16-19。（ATR-遠紫外分光装置については文献18a）を参照のこと）尾崎研の遠紫外分光の研究で最も重要な成果は、凝縮相においてもRydberg遷移が存在することをはっきりと示したことである。いずれの有機化合物のアルカンやケトンなどの遠紫外スペクトルにおいても、Rydberg遷移を含めて考えなければ、説明できないバンドが観測された16-19。量子化学計算でRydberg遷移を取り扱う場合は、時間依存密度汎関数 (Time-dependent Density Function Theory, TD-DFT) 法では汎関数にはCAM-B3LYP法を、基底関数には分散関数を加えることでよい結果が得られた20-24。アルカン20,21、アミド22に関しては波動関数理論であるSAC-CI(Symmetry adapted cluster/configuration interaction)法を用いてもRydberg遷移の存在を確認できた。

森澤、江原らによるn-アルカンの量子化学計算の研究については本ＨＰの「遠紫外分光」のところで紹介した。そこにATR-遠紫外分光法と量子化学計算で明らかになった遠紫外域における遷移もまとめた。

具体的な量子化学計算の例として Nylonの電子スペクトルと電子遷移の研究について紹介する。図1 (a)はα-型nylon 6やnylon 6/6など5種類のnylonのキャスト膜とnylonのモデルであるN-methylacetamide (NMA)(液体)のATR-遠紫外スペクトルを示す24。一方、図1(b)は200 nm付近のバンドで規格化した5種類のnylonのスペクトルである。いずれのnylonもalkyl基による吸収を150 nm 付近に、amide基による吸収を200 nm付近に示すが、NMAは当然amideによるバンドしか示さない24。Nylonのバンドはnylonの種類に依存するシフトと強度変化を示した。

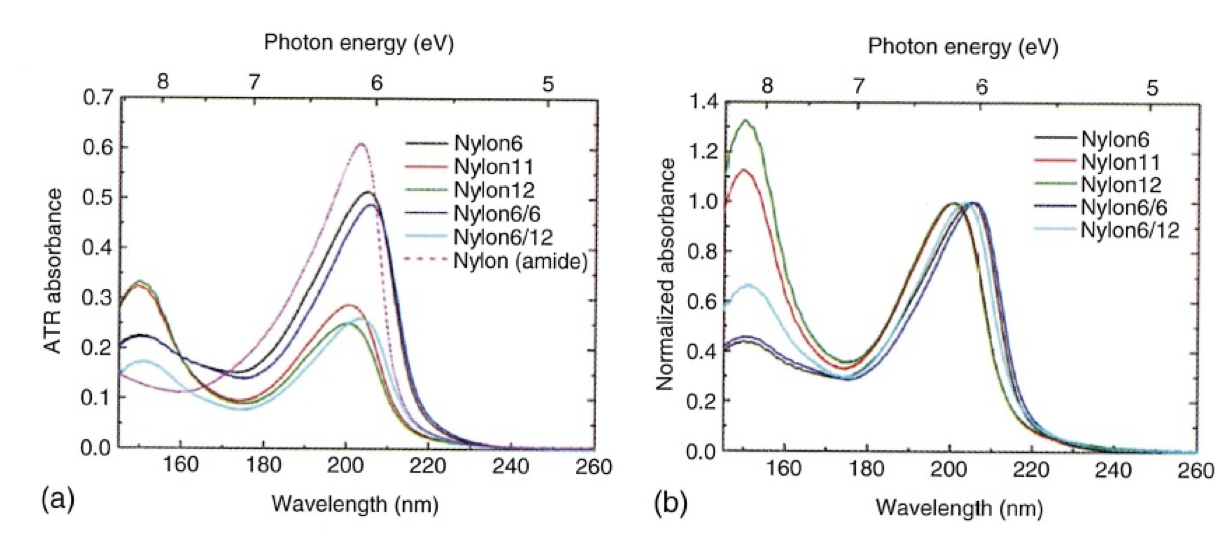
図1 (a)α-型nylon 6やnylon 6/6など5種類のnylonのキャスト膜とnylonのモデルであるN-methylacetamide (NMA)(液体)のATR-遠紫外スペクトル22。図1(b) 200 nm付近のバンドで規格化した5種類のnylonのスペクトル24。

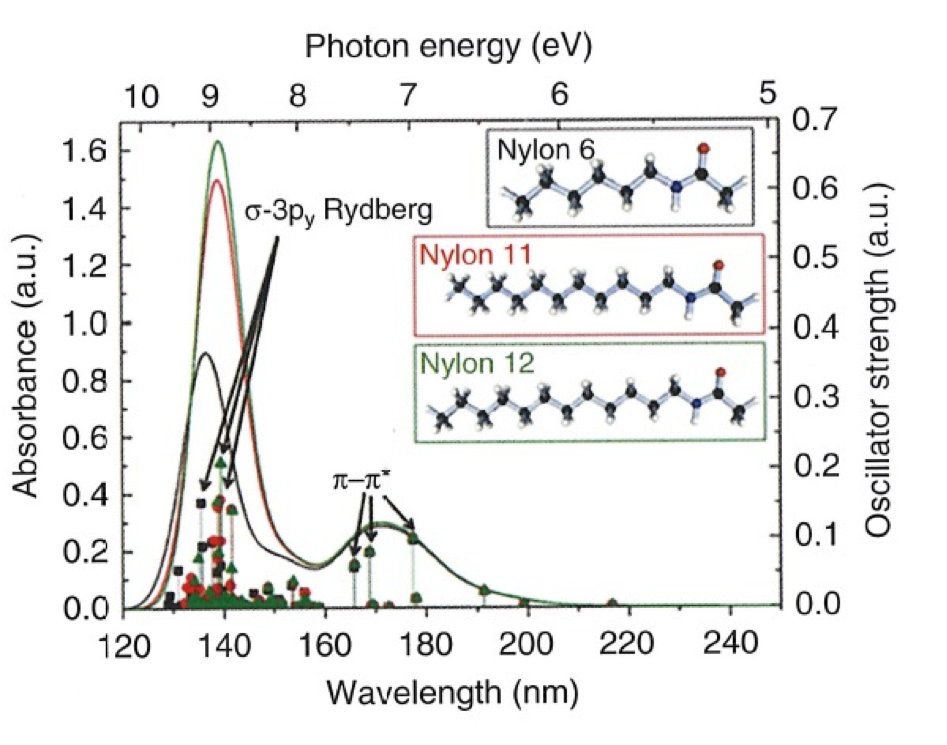
図2 nylon 6, nylon 11, nylon 12のモノマーユニットを用いた量子化学計算(TD-DFT)結果24。

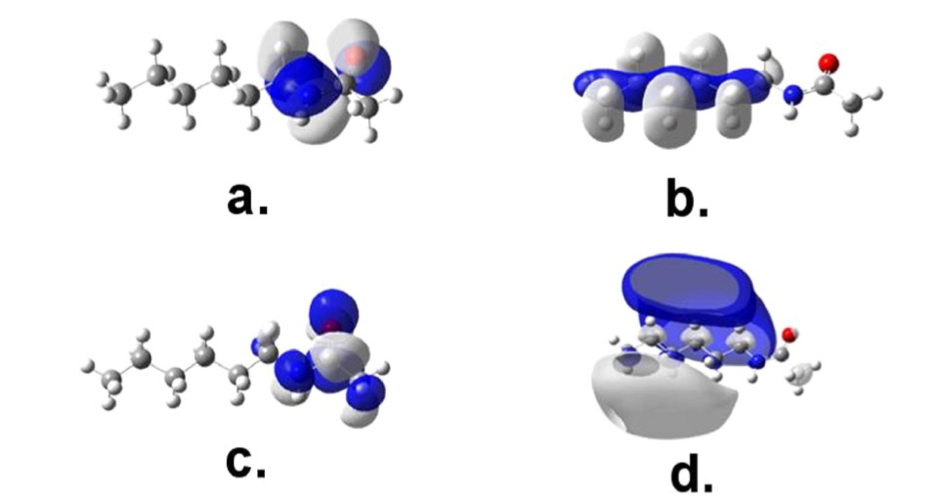
図3 量子化学計算で得られたKohn-Sham軌道の等電子密度面。a. HOMO-4, b. Rydberg3py, c.π-orbital, d.π*-orbital.24。

Nylonのスペクトルを解析するために、nylon 6, nylon 11, nylon 12のモノマーユニットを用いて量子化学計算(TD-DFT)を行った。その計算結果と計算で得られたKohn-Sham軌道の等電子密度面を図2, 図3に示す24。図2のシミュレーションスペクトルにある140と170 nmのバンドはそれぞれσ-3py Rydberg遷移とπ-π^*に帰属される。図3に示すように、Rydberg 遷移 (HOMO-4→Rydberg 3py)はalkyl鎖に非局在化しているのに対し、π−π* 遷移はamide基に比較的局在化していることが分かった。この例のように森澤ら24は、量子化学計算から電子遷移においても一定の原子団ごとに遷移が現れるということを示した。さらに量子化学計算 からα-型のnylon-6とnylon-6/6の遠紫外スペクトルにおけるπ-π^* 遷移によるバンドの長波長シフト(2 nm, 図 1)は、結晶構造と分子間水素結合の違いによるものであることが明らかになった。これらの違いは、π-π^* 遷移の局在化の違いや遷移双極子カップリングの違いとしても現れる24。

森澤らは固体状態におけるアルカンの分子間相互作用を調べるために、常温で液体のn- tetradecane（C14H30）を融点以下まで冷却し、相転移前後のスペクトル変化を観測した25。図4はn- tetradecaneの遠紫外スペクトルの温度変化 (18〜-38℃, (a) cooling 過程と(b) heating過程)を示す23。153 nmのバンドの強度は融点 (6℃) 以下で単調に減少する。一方、200と230 nmのバンドは融点付近で現れ、その後、単調に増大する。この温度変化は可逆的である。この実験結果を解析するために、森澤ら25はn-pentane ダイマーのスペクトルのシミュレーションを行った。ダイマー間の距離を変えて計算した計算結果が図5である。ダイマー間の距離を6Åにとると、常温のn- tetradecaneのスペクトルによく似たスペクトルが得られた。ダイマー間の距離を3Åまで縮めると固体状態のモデルとなり、-38℃のn- tetradecaneのスペクトルによく似たものが得られた25。3つの主なバンド(153, 200, 230 nm)の波数位置や強度は十分には再現できていないが、153 nmの吸収が、以下に述べる理由により、長波長側へ大きくシフトすることを証明できた。この長波長シフトの原因は、実験結果と量子化学計算の結果から、外側に張り出したσ軌道、HOMO-1およびHOMO-2軌道が固体中の分子間相互作用により不安定化軌道と安定化軌道を作り、この2つの軌道間の遷移のエネルギーが小さくなる(HOMO-LUMO ギャップの縮小)ことによることが分かった。このようにσ軌道の変化による遷移の変化を実験的に観測した例は遠紫外分光ではこれまでにない25。

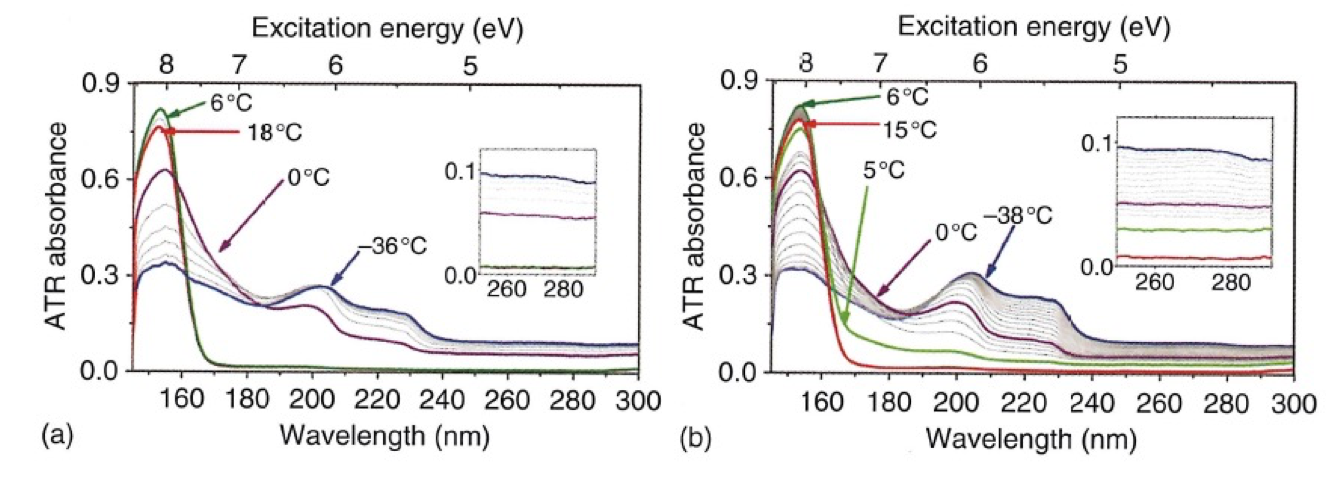
図4 n- tetradecaneの遠紫外スペクトルの温度変化 (18〜-38℃, (a) cooling 過程と(b) heating過程)25.

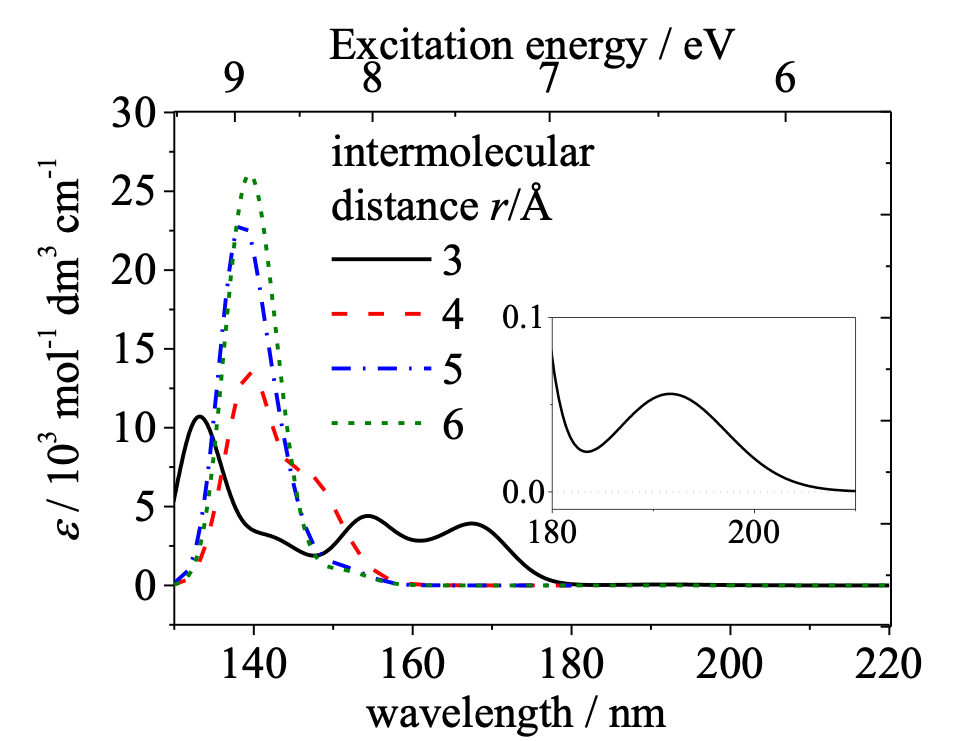
図5 n-pentane ダイマーのスペクトルのシミュレーション。ダイマー間の距離を変えて計算した計算結果25.

田邉ら26は遠紫外/深紫外分光法と量子化学計算法を用いていろいろなイオン液体の電子状態の研究を行った。イオン液体の中にはammonium系カチオン(N,N,N-Trimethyl-N-propylammonium: [TMPA]+) とamide系アニオン (Bis (trifluoromethylsulfonyl) amide: [TFSA]-から構成される[TMPA][TFSA]のように、遠紫外域にしか吸収を示さないものもある。一方、[TFSA]-アニオンとimidazolium系カチオン(1-Butyl-3-methylimidazolium: [BMIM]+ から構成される[BMIM] [TFSA]や[BMIM]Iのように遠紫外域と深紫外域の両方に吸収を示すものもある。図6はこれらのイオン液体のATR-遠紫外/深紫外/紫外可視スペクトルである26a。

これらのスペクトルを解析するために量子化学計算が行われた26a。構造最適化は、I原子に対してはSadlej pVTZ basis set を用いた B3LYP法を、他のものについてはcc-pVTZ basis setを用いたB3LYP法を用いた。遷移エネルギーの計算は、I原子に関しては、Sadlej pVTZ basis set を用いた TD-CAM-B3LYP法を、他のものについてはaug-cc-pVTZ basis setを用いたTD-CAM-B3LYP法を用いた。

[TMPA][TFSA]の吸収スペクトルは150 nm付近にのみバンドを示す（図6(a))。 TFSAを含む類似のイオン液体[BMPY][TFSA](BMPY; 1-Butyl-3-methylpyrrolidinium)や[TOMA][TFSA](TOMA; N,N,N’-Trioctyl-N-methylammonium)のスペクトルも150 nm付近にのみバンドを示した。このバンドはTFSAの量子化学計算から、HOMO-1からLUMO+3への遷移とHOMOからLUMO+1への遷移であることが分かった（図6(a))26a。図6(c)に示す[BMIM] [TFSA]や類似のイオン液体 [BMIM][BF4], [EMIM][TFSA] (EMIM; 1-Ethyl-3-methylimidazolium), [EMIM][BF4] などはいずれも170 と210 nm 付近に吸収を与える。これらは主にカチオン内の電子励起に帰属されることが分かった。Imidazolium系のカチオンとhalogen (Cl, Br, I) 化物アニオンの組み合わせでは、アニオン内やカチオン内の電子励起による吸収に加えて、アニオン―カチオン間の電荷移動による吸収が長波長側に確認された図6(e)）。 以上のように遠紫外/深紫外スペクトルの測定と量子化学計算からイオン液体の電子状態に関する新しい知見が得られた26a。田邉らはこの研究をさらに発展させ、電気化学-ATR遠紫外/深紫外分光法を用いたイオン液体の研究を行っている26b。

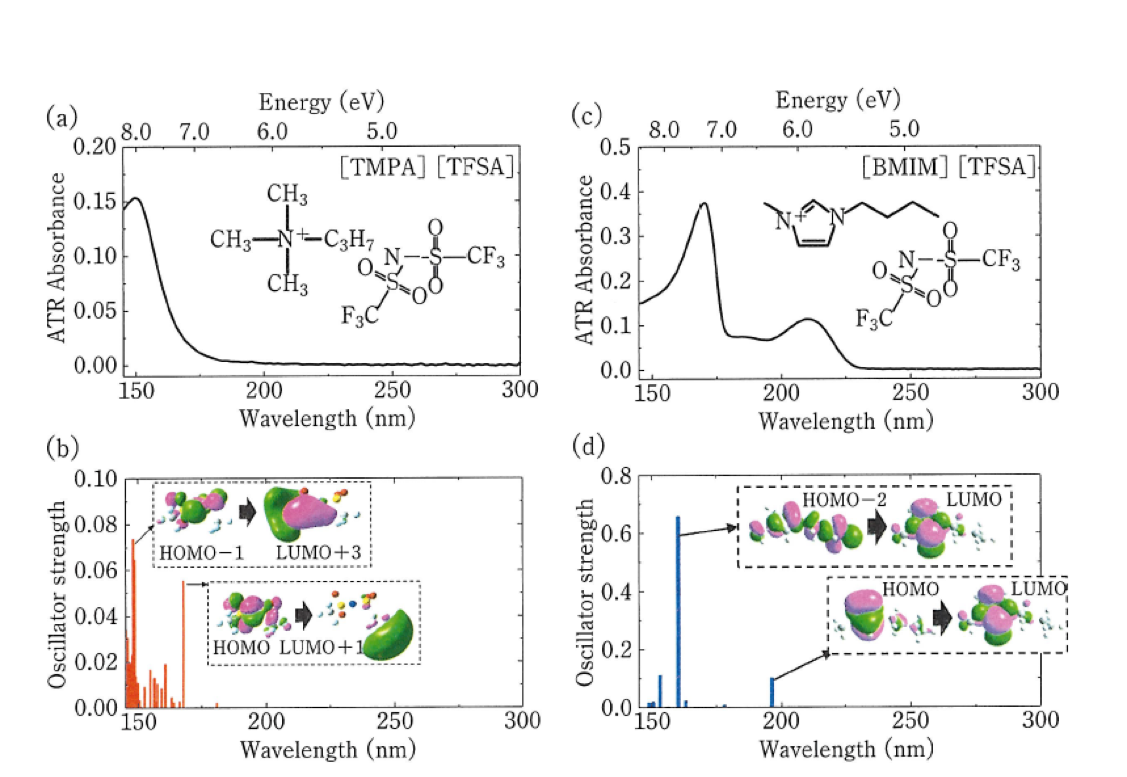
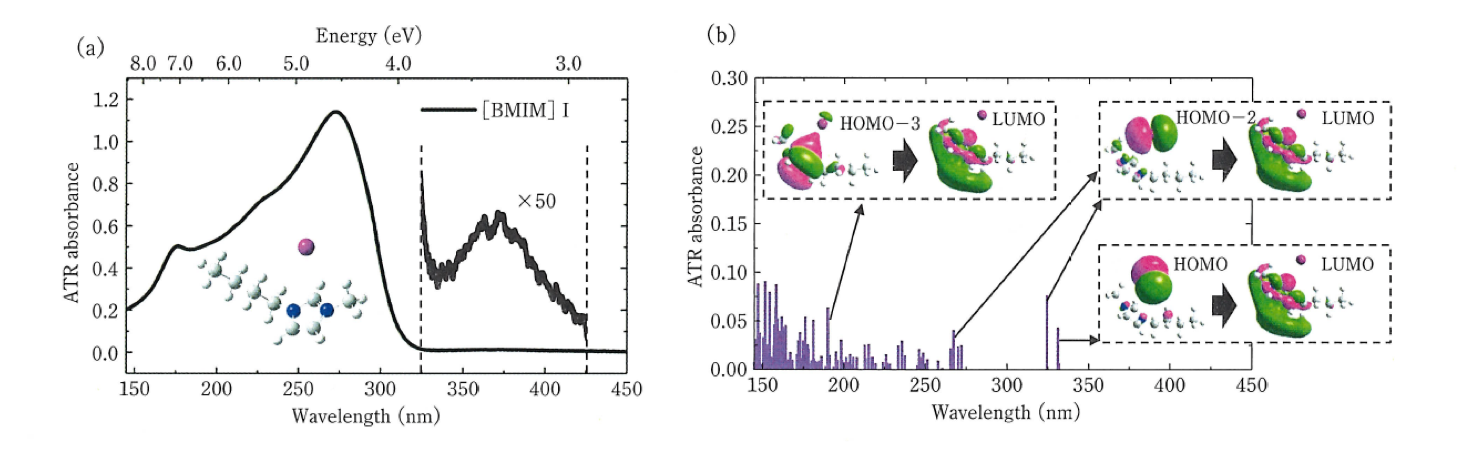
図6イオン液体のATR-遠紫外/深紫外/紫外可視スペクトル26a。

(a),(b) [TMPA][TFSA]の遠紫外スペクトルとDFT 計算の結果. (c),(d) [BMIM][TFSA] の遠紫外スペクトルとDFT 計算の結果. (e),(f) [BMIM]I の遠紫外スペクトルとDFT 計算の結果.

Becら27は遠紫外/深紫外分光法と量子化学計算を用いてgrapheneの電子状態の研究を行った。grapheneの遠紫外/深紫外スペクトルにはπ-π* 遷移による4.7 eV(270 nm)のブロードなピークのほかに、7.5 eV (170 nm)（graphene flake）と 6.7 eV(180 nm)（nano platelet）にバンドが観測された。遠紫外域においてgrapheneのバンドが観測されたのは、おそらくこれが初めてであろう27。この実験結果を説明するために、grapheneのモデルを用いてTD-DFT法とグラフェンの計算に良く用いられるZINDO (Semi-empirical calculations at Zerner's Intermediate Neglect of Differential Overlap) 法によりgrapheneの電子状態の量子化学計算が行われた27。スペクトルの再現は、ZINDO法の方が良い結果を与えた。分子モデルの量子化学計算から、深紫外域における遷移に比べ、遠紫外域における遷移に関係した励起状態の電子密度はより非局在化していることが分かった。さらに、graphene平面の大きさやそれらの空間的配置は電子状態のスペクトルに強く反映されるが、grapheneの層数はスペクトルにはあまり影響しないことが明らかになった27。

このほかにBecら28は遠紫外/深紫外分光法と量子化学計算法を用いて、Rydberg遷移がgraphene nanocompositeの構造変化と相転移のプローブとなることを示した。

分子の赤外スペクトルのシミュレーションは、調和振動計算と経験的スケーリングを用いてかなり良い結果が得られる場合も多い9,10。最近は非調和性を含む計算も盛んにおこなわれるようになってきた9,10,13b,29,30。非調和性を含むDFT計算はかなり以前から提案されていたが、なかでもVSCF 法はよく知られている12。この方法では、完全な振動波動関数を一組の基準モード波動関数に分解する。VSCF法の改良版としてはPerturbation-corrected VSCF (PT2-VSCF) 法がある31。この方法はやはり2次の摂動論を用いてVSCFよりもより高精度な計算結果を与える。さらに計算の正確さと計算リソースとのバランスに優れているものとして2次の振動摂動論に基づくVibrational perturbation thory (VPT2)法がある32。

Becら33,34は赤外域における量子化学計算で二つの常用な研究を行った。非結合音の赤外スペクトルへの影響の研究と結晶構造に基づく周期的調和振動計算と小さなモデルを用いた非調和計算によるその補正の研究である。

Becら33は非基本音の赤外スペクトルへの影響をテーマに非調和性を考慮したDFT計算を用いて脂肪族エーテルの赤外スペクトルの研究を行った。7種類の脂肪族エーテル（di-n-propylether, DNPE; di-iso-propylether, DIPE; n-butylmethyl ether, NBME; n-butylethyl ether, NBEE, di-n-butyl ether, DNBE; tert-buytlmethyl ether, TBME; tert-amylmethyl ether, TAME）の基本音、第1倍音、結合音の振動数と強度を代表的な非調和計算法のひとつであるGVPT2 (generalized vibrational second-order perturbation theory) を用いて計算した (DFT-B2PLYP/SNST level) 33。GVPT2法は一般的な形式で、２次の振動摂動論を実装したもので、Darling-Dennison共鳴やFermi共鳴の取り扱いを含む完全な非調和計算に対する効率的で正確な方法である35。最近、赤外、近赤外の分野で注目されている。上述の各Ether化合物についての赤外スペクトルの計算はそれぞれの構造異性体について行われた。この研究で重要なポイントの１つは１次（例えば、Darling-Dennison共鳴）、２次（例えばFermi 共鳴）の振動共鳴である。

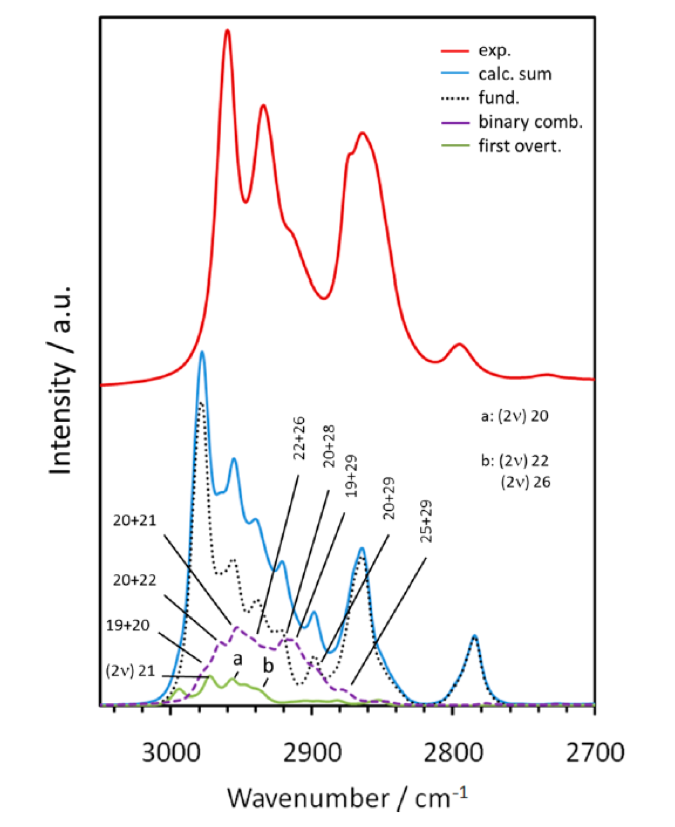
図7 DNBEのC-H伸縮振動の領域 (3050-2700 cm-1) の実験、計算赤外スペクトルの比較33。

3050-2700 cm-1の領域：図7はDNBEのC-H伸縮振動の領域 (3050-2700 cm-1) の実験、計算赤外スペクトルを比較したものである33。計算スペクトルは10個の構造異性体の寄与を含んでおり、おおむね実験スペクトルをよく再現している。この領域には非基本音、とくに結合音によるバンドが大きく寄与する。Methylene基の変角振動、とくにはさみ振動や縦揺れ振動、methyl 基の縮重変角振動を含む結合音が現れる（図7）。図7には基本音と、結合音、第1倍音の寄与を比較して示した。結合音が2980-2880 cm-1の領域に大きく寄与しているのが分かる。倍音の寄与も無視できない。これらの非基本音の寄与は実験スペクトルのバンド形に大きな影響を与えていることがわかる。とくに、2980-2880 cm-1の領域の吸収の増大に大きな影響を与えている。

2700-1500 cm-1の領域：図8(a)はDNBEの2700-1500 cm-1の領域の実験、計算赤外スペクトルを比較したものである33。この領域に観測されるバンドはすべて結合音、倍音によるものであるが、計算スペクトルは、振動数、強度、バンド形のいずれにおいても実験スペクトルをよく再現している。比較的強度の強い2404, 2086, 1953 cm-1の3本のバンドは、それぞれ、2404 cm-1 (νCO +δtwistCH2, δtwistCH2 +δasCH3, νCC +δwaggCH2, νCO +δwaggCH2), 2086 cm-1 (CC +νCO, δrockCH3 +νCO, δrockCH2 +νCO), 1953 cm-1 (νCC +νCO, δrockCH2 +νCO, δCCC +δscissCH2) に帰属される。これらのバンドは結合音の中では、比較的強く観測されているが、それは比較的遷移双極子モーメントの大きいC-O伸縮振動の強い寄与を含んでいるからである。

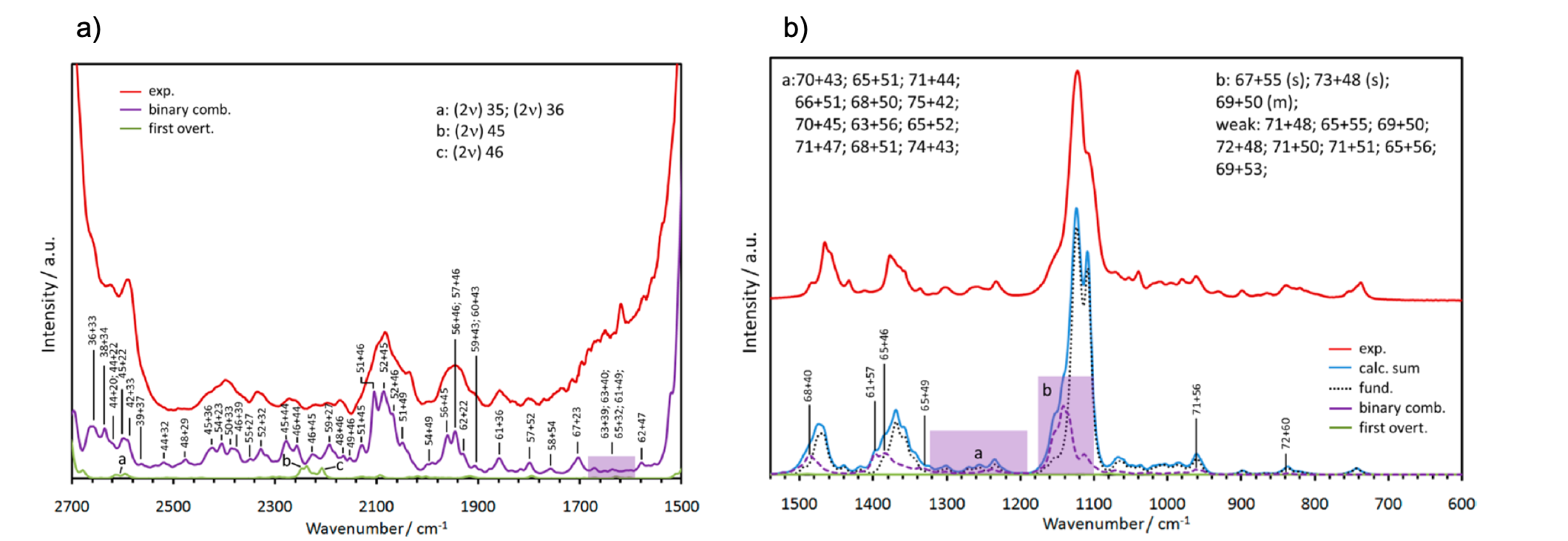
図8 a) DNBEの2700-1500 cm-1の領域の実験、計算赤外スペクトル32。b)1500-600 cm-1の領域の実験スペクトルと計算スペクトルの比較33。

1500-600 cm-1の領域：1500-600 cm-1の領域の実験スペクトルと計算スペクトルの比較を図8b)に示した33。この領域で非調和性の影響が目立つのは1180-1080 cm-1のC-O伸縮振動の領域である。Becら33は非調和GVPT2法を用いて倍音、結合音の脂肪族エステルの赤外スペクトルへの影響を明らかにした。非基本音が赤外スペクトルのバンド形を決めるうえで非常に重要な役割を果たしていることは分かっていたが、今回の研究は赤外の全領域でそれを詳細にわたり解析したと言える。

Becら34は、結晶構造に基づく周期的調和振動計算と小さなモデルを用いた非調和計算によるその補正を用いて核酸塩基結晶の赤外スペクトルの解析を行った。彼らは最初に結晶の周期的モデルに対して調和振動計算を行い、その計算結果に小さなモデル（核酸塩基のモノマーやダイマーなど）に対する非調和計算による補正を加えるという方法を用いて4種類の核酸塩基の結晶状態の赤外スペクトルのシミュレーションを行った。その結果、倍音、結合音が赤外の指紋領域にかなり寄与していることが明らかになった。Becらはまず、核酸塩基の結晶の周期モデルを用いて調和近似で基本音の振動数と強度を計算した34。そして小さなモデルついて非調和性を考慮した計算を行った。最後にそれらを併せて核酸塩基の赤外スペクトルを再現し、少数の小さなモデルに対する非調和計算が、大きな結晶系の調和計算の結果を、効果的かつ安価に補正する方法を与えることを示した。Becら34はこの研究でとくに1800-1600 cm-1の領域の研究に力点を置いた。それは振動共鳴など非調和性の効果の重要性が実験（例えばフェムト秒2D-IR36,37）と理論の両方でとくにこの領域に対して指摘されていたからである。実験スペクトルとの一致を良くし、バンドの帰属の信頼性を上げるために計算した調和振動赤外スペクトルはWLS 法によってスケール調整を行った。非調和性の計算は、DVPT2 (deperturbed vibrational second-order perturbation theory) を用いて行った。

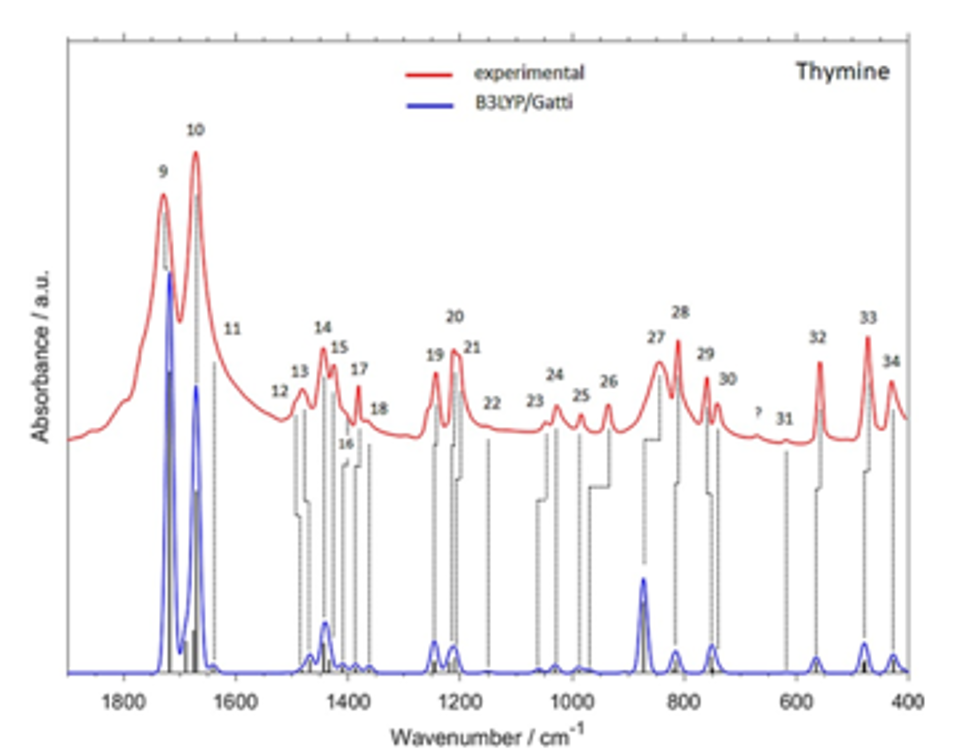
図9 thymine結晶の実験およびシミュレーションスペクトルの比較である（1800-400 cm-1の領域）34。

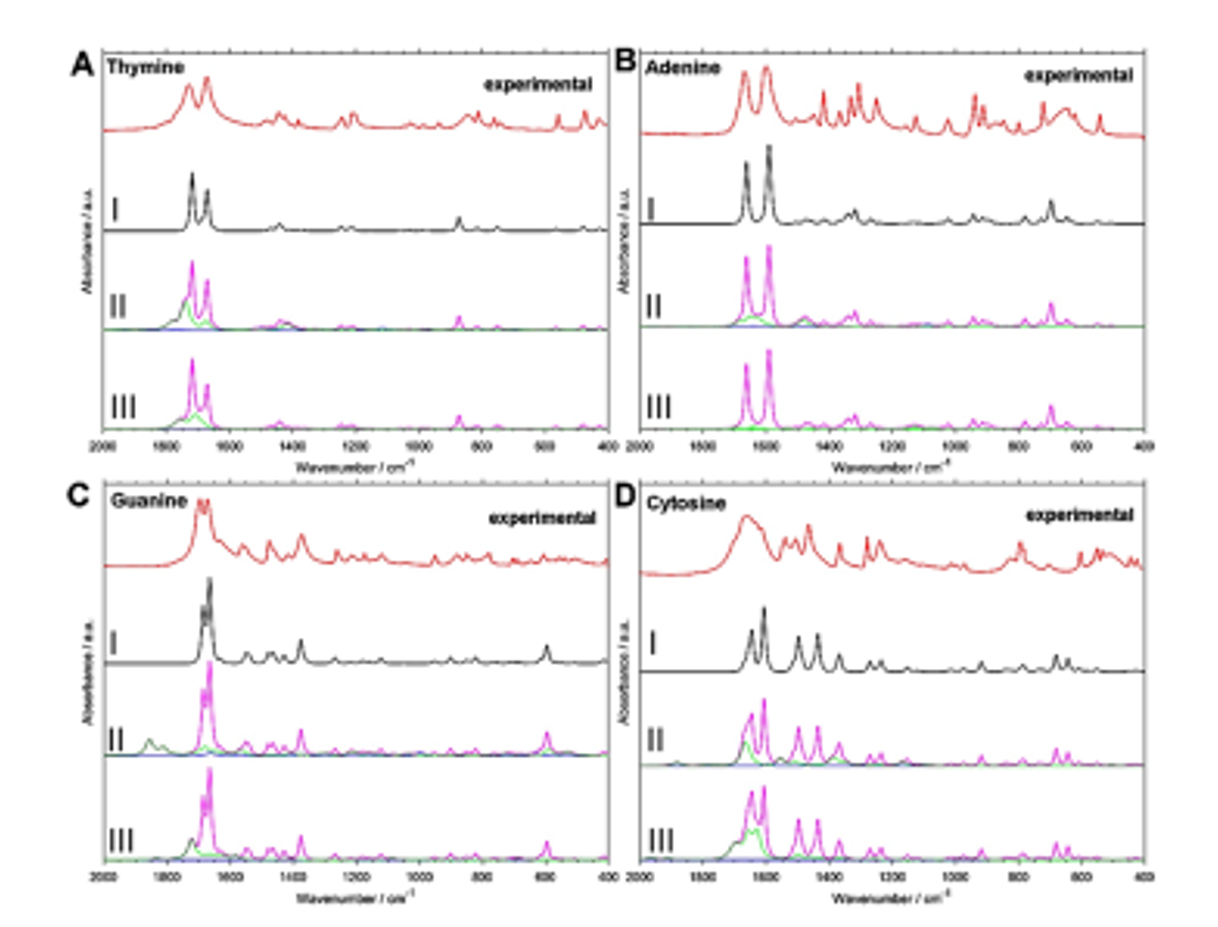
図10 4種類の核酸塩基の実験結果と3つの計算結果、すなわち調和振動計算 (I), (I)にモノマーに対する非調和計算で得た倍音と結合音の結果を加えたもの (II)、ダイマー に対する非調和計算で得た倍音と結合音の結果を加えたもの(III)34。

図9はthymine結晶の実験およびシミュレーションスペクトルの比較である（1800-400 cm-1の領域）34。シミュレーションスペクトルはthymine結晶に対してB3LYP/Gatti Levelでの周期的DFT計算で行われたものである。計算結果は、振動数、相対強度ともに実験結果を良く再現している。1729と1671 cm-1に観測される強いバンドは、それぞれNH面内変角振動とCN変角振動のカップリング、面内環変角振動に帰属された。図10は4種類の核酸塩基の実験結果と3つの計算結果、すなわち調和振動計算 (I), (I)にモノマーに対する非調和計算で得た倍音と結合音の結果を加えたもの (II)、ダイマー に対する非調和計算で得た倍音と結合音の結果を加えたもの(III)である34。(II),(III)の緑と青の線はそれぞれ結合音と倍音による寄与を表す。（II）のスペクトルは1800-1600, 1500-1400 cm-1のいずれの領域においても実験スペクトルにより近い結果を与える。モノマーを用いた方がダイマーを用いた方よりもより良い結果を与えたが、guanineだけはダイマーモデルがより良い結果を与えた(III)。これらの結果は、モノマーを用いた非調和計算の結果による調和振動計算の結果の補正が非常に有効であることを示している34。

ここで提案したBecら34の方法は、広範囲な分子に対して適用できるきわめて一般的な方法である。

量子化学計算を用いた近赤外分光法の研究は、本HPの「近赤外分光法」のところにもある。近赤外スペクトルには分子振動の倍音、結合音によるバンドが観測されるが、倍音、結合音の振動数や強度を解析することにより振動ポテンシャルや非調和性について研究することができる1,5,6。しかし倍音、結合音の帰属や強度の解析は非常に複雑であるため、これまで倍音、結合音に含まれる情報を的確に抽出することが難しかった。最近、非調和性を考慮した量子化学が急速に進化し、倍音のみならず、結合音の振動数や強度も研究できるようになった38-40。これにより近赤外分光法の物理化学や溶液化学への応用が活発になってきた。

赤外、ラマンスペクトルのシミュレーションの場合と異なり、近赤外スペクトルのシミュレーションの場合はもちろん調和振動計算は使えない。近赤外スペクトルのシミュレーションは非調和計算の難しさと計算リソースの不足のため最近までほとんど行われなかった。非調和性を含むDFT計算による近赤外スペクトルのシミュレーションとバンドの帰属を行ったのはおそらく尾崎研究室Becらのものが最初であろう30,38-40。近赤外スペクトルの計算に良く用いられる非調和計算法はVSCF法とVPT2法である。とくに後者は比較的安価短時間で優れた精度の計算結果を与える。

非調和を含む計算法には2重の利点がある。すなわち単一モードの非調和性とマルチモードの非調和性である。前者は基本音によるバンドに対してより正確な振動数と強度を与えるとともに倍音を予測する。一方、後者はモード―モードカップリングを記述する。このモード―モードカップリングは結合音と振動共鳴を再現する。

Becら30,38-41は主にDVPT2法を用いてアルコール、脂肪酸、核酸塩基、天然物化合物など一連の有機化合物の近赤外スペクトルのシミュレーションを行った。脂肪酸については酢酸から始めて中程度の大きさの脂肪酸、長鎖脂肪酸について計算を行った39,40。図11A,B,C,D,E,Fはそれぞれ飽和と不飽和長鎖脂肪酸の実験スペクトルとシミュレーションスペクトルの比較である40。細部を除けば両者はかなり良い一致を示している。しかしOH伸縮振動の第一倍音の波数は必ずしも良い一致を示していない。それはこのモードが非調和性が大きく、DVPT2法が非常に非調和性の高いモードの取り扱いに必ずしも十分でないからである40。実験スペクトルとシミュレーションスペクトルの6200-5400 cm-1の領域を拡大したのが、図12である。やはりA,B,C,D,E,Fはそれぞれ飽和と不飽和長鎖脂肪酸の結果を示す。飽和脂肪酸の場合 (A,B,C)、この領域に観測されるのは、主にCH3とCH2の伸縮振動の結合音である。これらのモードの第1倍音は非常に弱い（図12の緑の部分を参照のこと）。不飽和脂肪酸の場合 (D,E,F) はCH3とCH2の伸縮振動の結合音のほかに、CH伸縮振動の第1倍音や結合音も観測される。図の緑の部分がやや大きくなることに注意せよ。

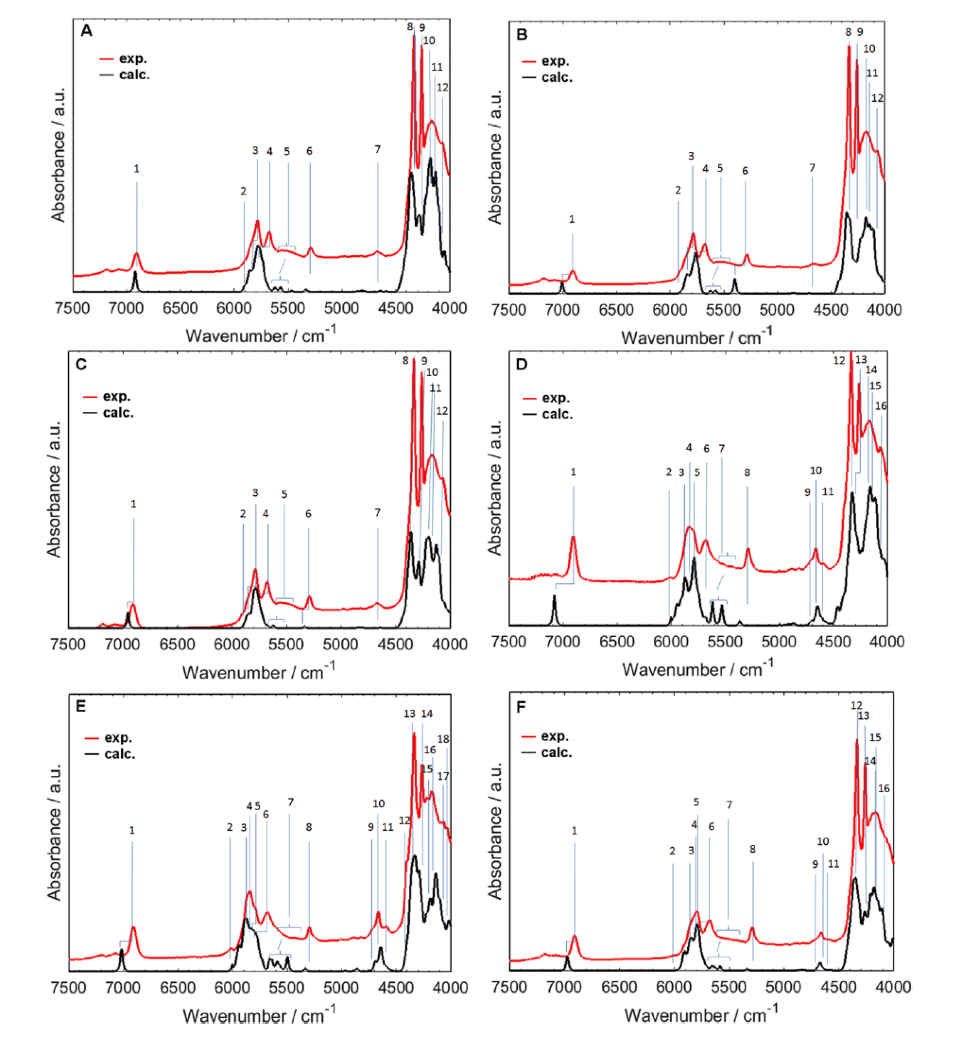
図11　飽和と不飽和長鎖脂肪酸の実験スペクトルとシミュレーションスペクトルの比較40。(A) arachidic acid, (B) palmitic acid, (C) stearic acid, (D) linoleic acid, (E) α-linolenic acid, (F) oleic acid.

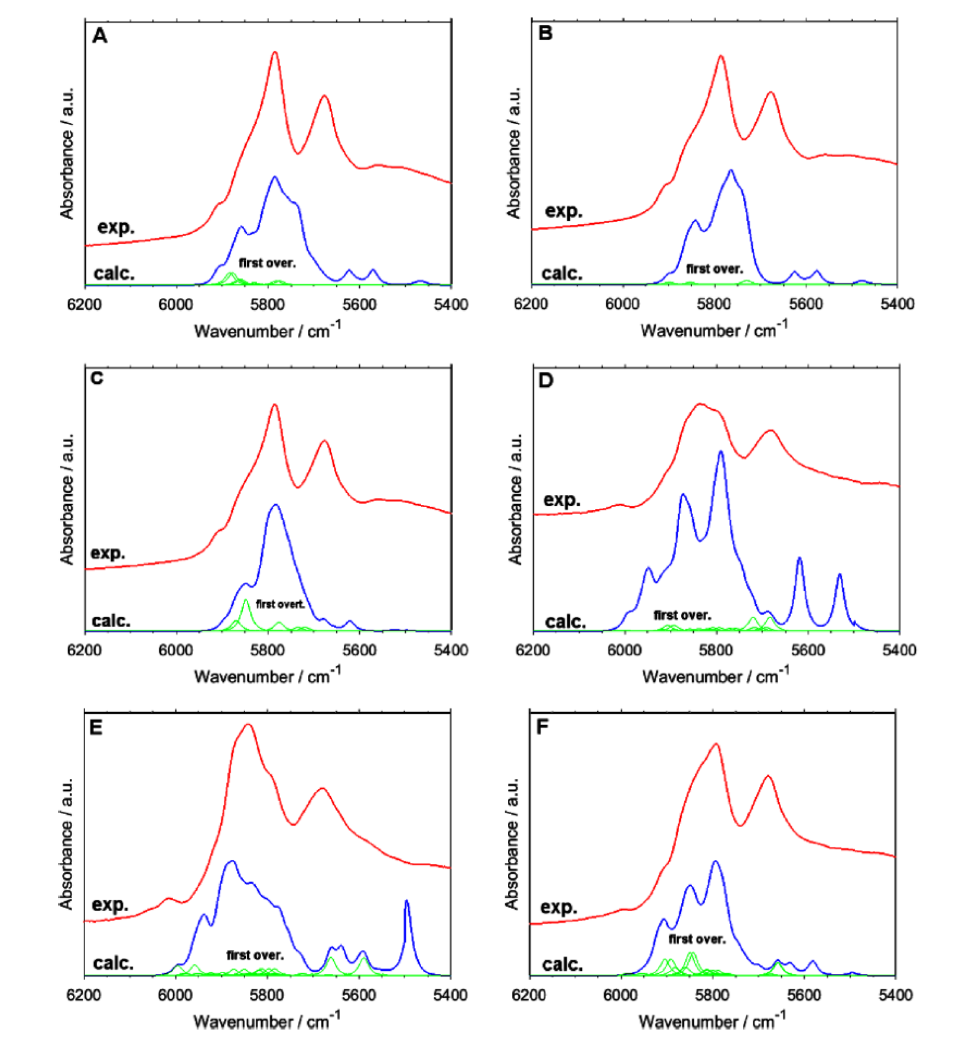
図12 図11の実験スペクトルとシミュレーションスペクトルの6200-5400 cm-1の領域の拡大40。

DVPT2法は複雑な分子の近赤外スペクトルの計算に有用であることが分かった。しかし非常に非調和性の高いモードの取り扱いについては必ずしも十分な結果を与えない。モノマーのOH伸縮振動の第1倍音の振動数のずれなどを見ればわかる。Becら41はこの他にもいろいろな基本的な分子だけでなく、薬用植物, rosmaric acidなどやや分子量の大きな分子の近赤外スペクトルのシミュレーションにも成功している41。これからはいろいろな分子の近赤外スペクトルのシミュレーションやバンドの帰属が非調和DFT計算で可能になろう30。

二見ら42,43は近赤外スペクトルに対する水素結合と溶媒効果の影響を量子化学を用いて調べた。分子振動の非調和性や振動ポテンシャルは、分子間、分子内相互作用、溶媒効果などが敏感に反映される。これまで主に赤外、ラマン分光法を用いて水素結合や溶媒効果の研究が行われてきた。しかし赤外、ラマン分光法では、時として水素結合形成と溶媒効果など誘電場の影響がバンドシフトに与える効果を区別することが難しい場合がある。二見ら42,43は、基本音の吸収強度の変化と倍音の吸収強度の変化を比較することにより、バンドシフトが水素結合と溶媒効果のどちらに由来するかを識別ができる可能性があることを示した。

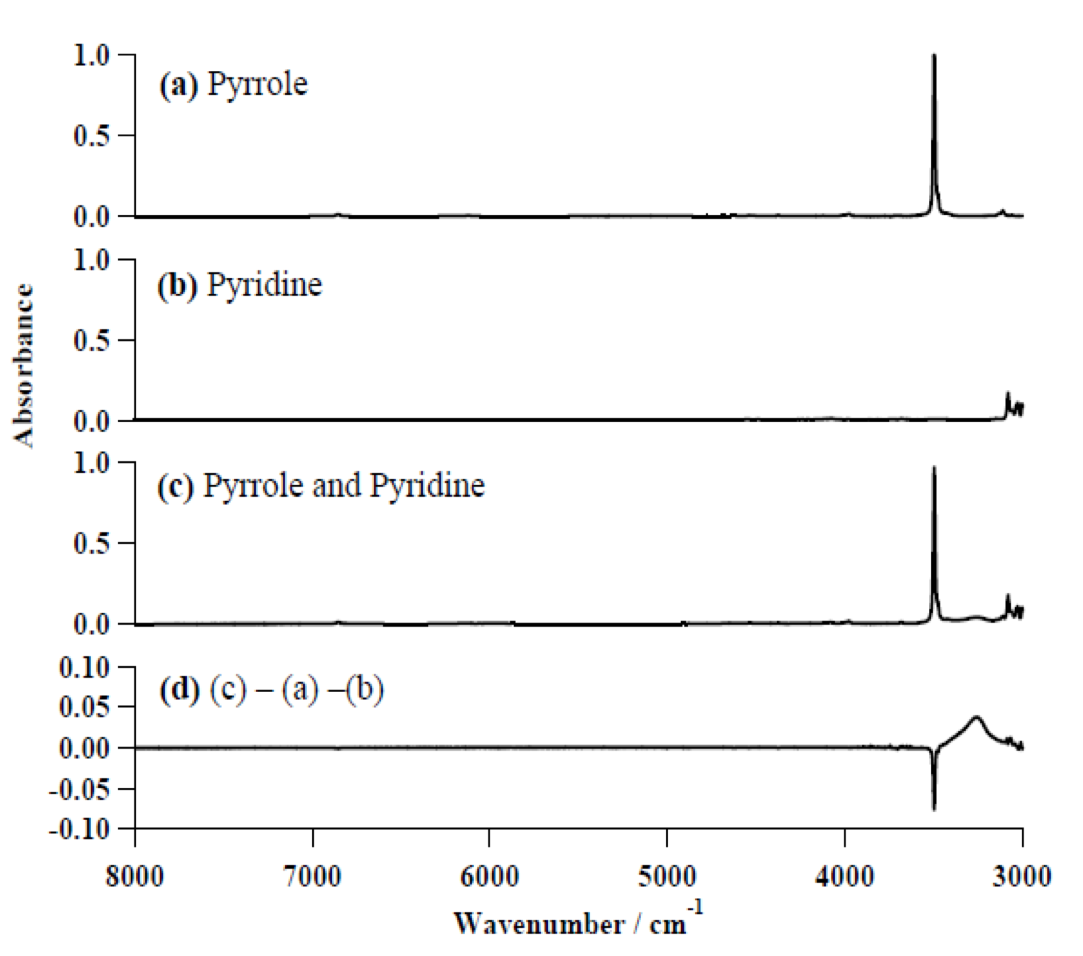
図13 (a) pyrrole, (b) pyridine, (c) pyrrole-pyridine complexの近赤外/赤外スペクトルの　8000-3000 cm-1の領域42。(d) ; (c) のスペクトルから (a) と (b) のスペクトルを差し引いた差スペクトル。

図13は (a) pyrrole, (b) pyridine, (c) pyrrole-pyridine complexの近赤外/赤外スペクトルの8000-3000 cm-1の領域である44。図13(d) は (c) のスペクトルから (a) と (b) のスペクトルを差し引いた差スペクトルを示す。差スペクトルから明らかなように、水素結合の形成 (pyrrole-pyridine complexの形成) に伴って、NH伸縮振動の基本音は低波数シフトし、ブロードで強くなっているのに対し、倍音はその強度がほとんど確認できないほどに弱くなっている。これらの結果を説明するために、二見ら42は一次元のSchreodinger波動方程式を用いて水素結合形成に伴うNH伸縮振動の振動ポテンシャル、振動エネルギー、波動関数、遷移双極子モーメントの変化を調べた。図14は (a) pyrroleと(b) pyrrole-pyridine complexについて、NH伸縮振動のポテンシャルエネルギー曲線、波動関数、振動エネルギー、双極子モーメント関数を比較したものである44。水素結合の形成に伴って、NH伸縮振動の振動ポテンシャル、振動エネルギー、波動関数、遷移双極子モーメントが大きく変化する様子が分かる。NH伸縮振動の双極子モーメント関数がとくに大きく変化しているので、二見ら42は倍音の強度減少にはこの遷移双極子モーメント関数の減少が重要な役割を果たしていると結論した。

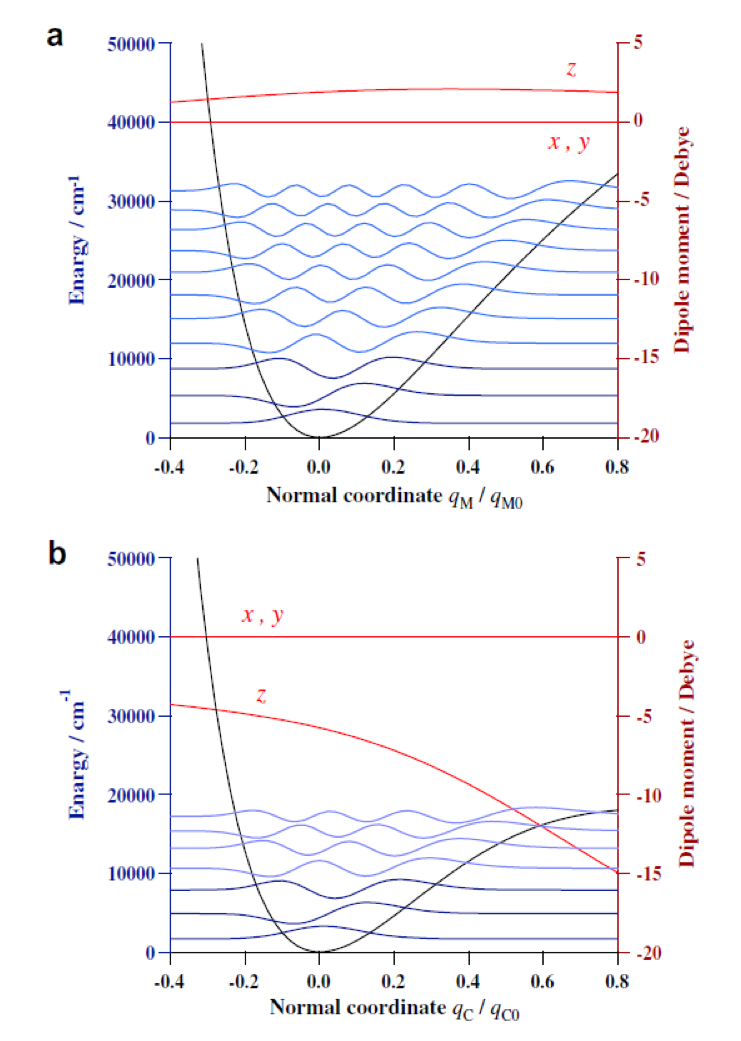
図14 (a) pyrroleと(b) pyrrole-pyridine complexについて、NH伸縮振動のポテンシャルエネルギー曲線、波動関数、振動エネルギー、双極子モーメント関数を比較したもの42。

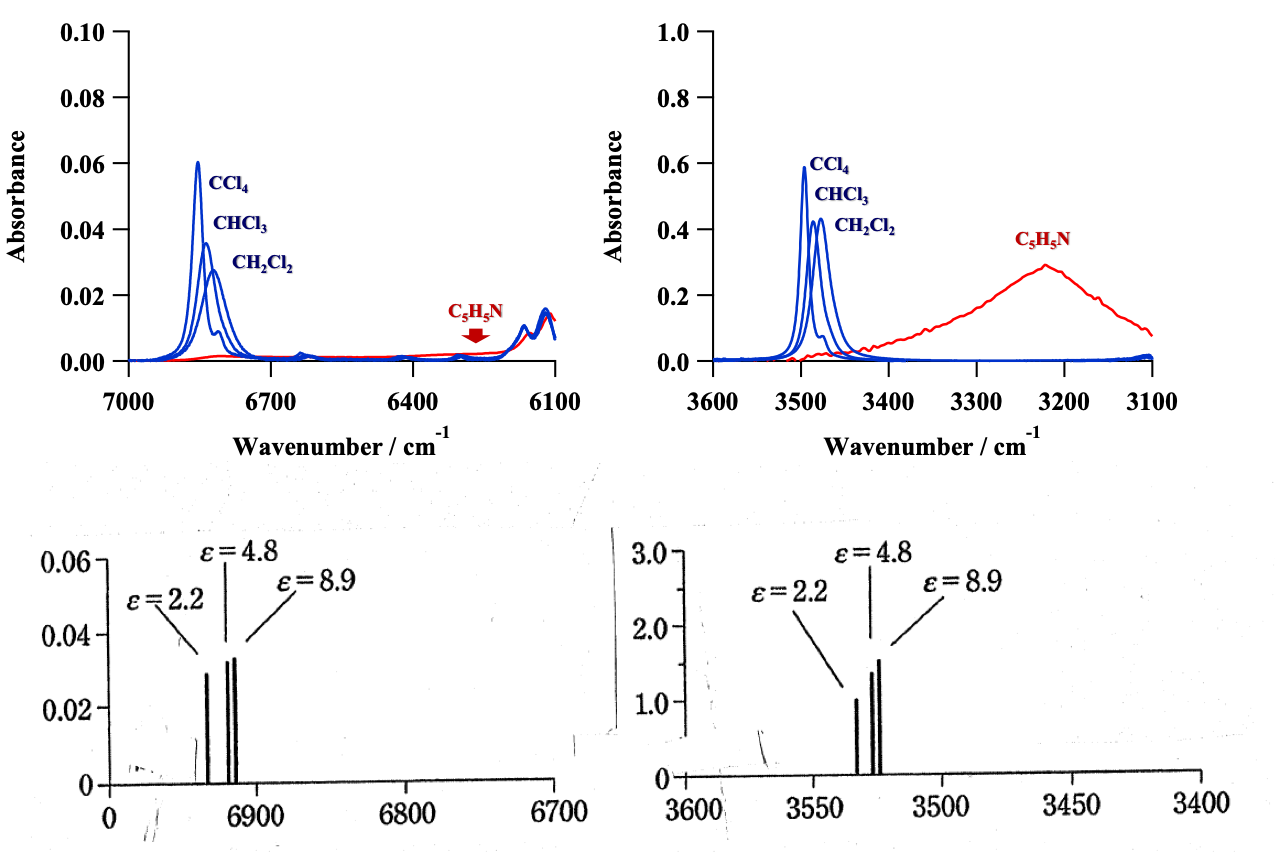
図15 pyrroleのCCl4, CHCl3, CH2Cl2溶液の (a)近赤外、(b)赤外スペクトル 連続誘電体モデルによるNH伸縮振動の振動数と波数の誘電率依存性の計算結果43

続いて二見ら43は溶媒効果の研究を行った。図15はpyrroleのCCl4, CHCl3, CH2Cl2溶液の(a)近赤外、(b)赤外スペクトルである。NH伸縮振動の基本音、第１倍音の振動数はともにCCl4, CHCl3, CH2Cl2の順に減少している。この順は誘電率が増大する順である（CCl4, CHCl3, CH2Cl2の誘電率は、それぞれ2.2, 4.8, 8.9である）。吸収強度は面積強度を見れば明らかなように、誘電率が大きくなるにつれ大きくなるが、その強度の増大は基本音でより顕著である。基本音の場合のみならず、倍音の場合も低波数シフトとともに強度が増大するという点が、水素結合の場合と異なる点である。図15 (a),(b)の下に、連続誘電体モデルによるNH伸縮振動の振動数と波数の誘電率依存性の計算結果を示す。計算結果は誘電率の増大に伴う低波数シフトと強度増大をうまく再現している。図16 は溶媒効果に関する量子化学計算の結果である43。 (a) はpyrrole のNH伸縮振動のポテンシャルエネルギー曲線、双極子モーメント関数 (ε=1-10)、波動関数 (ε=1) の誘電率依存性、(b) はポテンシャルエネルギー曲線の誘電率εが1の場合とその他の場合の差、(c)は誘電率が1の場合とその他の場合の双極子モーメント関数の差である45。これらの計算結果から、彼らは溶媒の誘電率の増加に伴うNH伸縮振動の基本音と第1倍音の振動数の減少は、振動ポテンシャルの非調和性からきていること、強度増大は双極子モーメント関数のスロープの緩やかな増大に起因するとした45。水素結合と溶媒効果は基本音では似た効果を与えるが、倍音では異なった結果を与えている。したがって基本音の変化と倍音の変化を比較することにより、いろいろな分子間相互作用を見分けることができる可能性がある42,43。

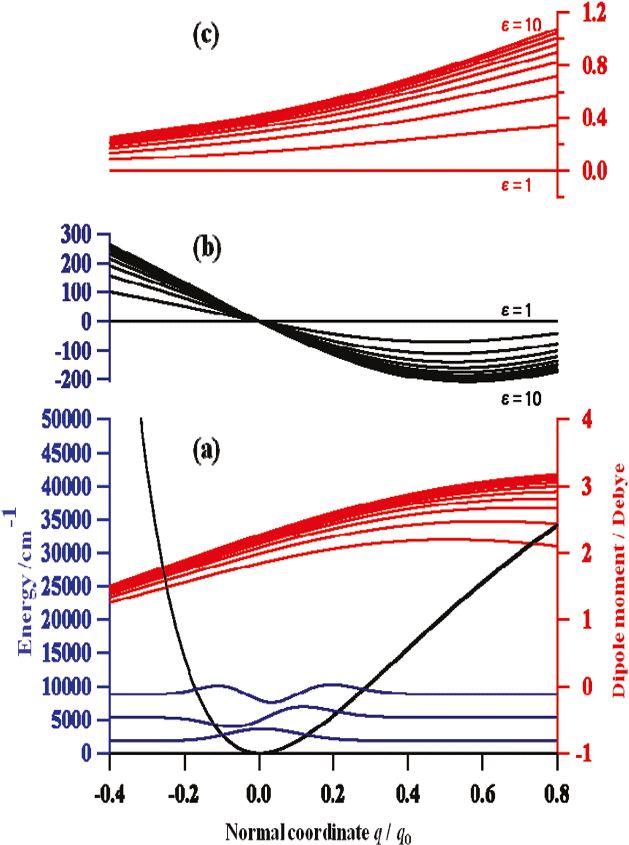
図16 (a) pyrrole のNH伸縮振動のポテンシャルエネルギー曲線、双極子モーメント関数 (ε=1-10)、波動関数 (ε=1) の誘電率依存性、(b) ポテンシャルエネルギー曲線の誘電率εが1の場合とその他の場合の差、(c) 誘電率が1の場合とその他の場合の双極子モーメント関数の差43。

尾崎教授らは近赤外分光法と量子化学計算を用いて高次倍音の研究を行った44-46。 言上ら44はphenolと2,6- dihalogenophenolの基本音、第1倍音、第2倍音、第3倍音の振動数と強度の研究を行い、それらのOH伸縮振動の振動数および吸収強度の振動量子数νへの依存性を調べた。さらにOH基の分子間、分子内水素結合について調べた。Phenol, 2,6-difluorophenol, 2,6-dichlorophenol, 2,6-dibromophenolのスペクトル測定には、溶媒としてn-hexane, CCl4, CHCl3, CH2Cl2を用いた。Phenolと2,6-difluorophenolは、溶媒であるCCl4, CHCl3, CH2Cl2と分子間水素結合を形成する。一方、　2,6-dichlorophenolと 2,6-dibromophenolは分子内水素結合を形成しやすい。図17はPhenol, 2,6-difluorophenol, 2,6-dichlorophenol, 2,6-dibromophenolのCCl4, CHCl3, CH2Cl2溶液のOH伸縮振動の強度の基本音、第1、第2、第3倍音による変化をプロットしたものである44。ここではn-hexane中のphenolのOH伸縮振動を強度の基準に取った。Phenolでは非常に興味深いことに、強度変化に興味深いν依存性が観測された。第1倍音 (ν=2) で弱くなったものが、再び第2倍音 (ν=3) で強くなり、第3倍音 (ν=4) では弱くなっている。同様の強度変化は2,6-difluorophenolでも観測されているが、残りのものでは観測されていない。Phenolと2,6-difluorophenolで不規則な強度変化が観測され、2,6-dichlorophenolと 2,6-dibromophenolで観測されないのは、前者では溶媒-溶質の相互作用が重要であるのに対し、後者では分子内水素結合が重要な役割を果たすからであると考えられる。Hoferと尾崎教授らは、最近、phenolのOH伸縮振動の強度変化についてcombined DFT/Numerov法を用いた電気的、力学的非調和性の考察から、ν依存性が確かに存在することを確認した45。

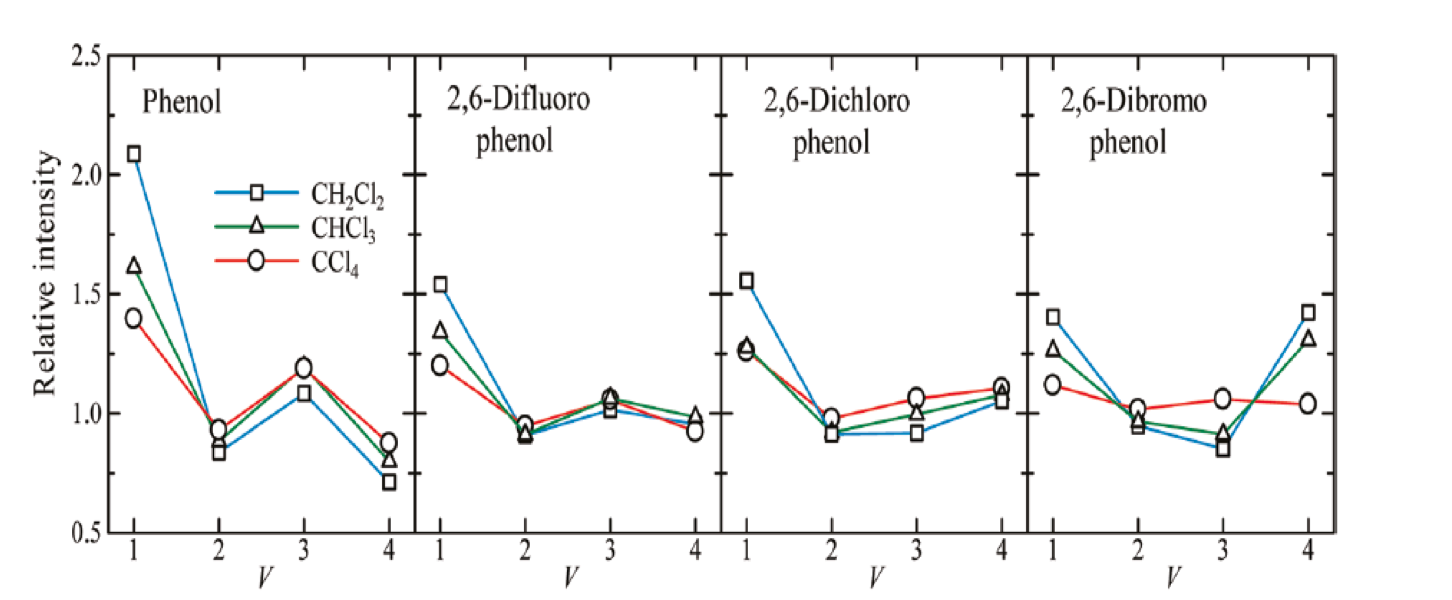
図17 Phenol, 2,6-difluorophenol, 2,6-dichlorophenol, 2,6-dibromophenolのCCl4, CHCl3, CH2Cl2溶液のOH伸縮振動の強度の基本音、第1、第2、第3倍音による変化のプロット44

Becら46は赤外、ラマン、近赤外（第1倍音、第2倍音）スペクトルと量子化学計算 (GVPT2/B3LYP, M06-2X, B2PLYP) を用いてCH3CN, CD3CN, CCl3CN液体の構造を調べた。

近赤外分光法の物理化学への応用は、振動ポテンシャル、非調和性、分子間相互作用など限りなくあるが、これまでは、あまり注目されてこなかった6。それは理論化学的考察が不十分であったからである。今後は理論化学の進歩にともない近赤外分光法の物理化学への応用が大きく発展すると思われる。

量子化学計算法を用いた遠赤外/テラヘルツ/低波数ラマンスペクトルの解析については、本HP「遠赤外/テラヘルツ/低波数ラマン分光法」に詳しく述べた。ここでは概略だけについて述べる。

量子化学計算法―遠赤外/テラヘルツ/低波数ラマン分光法を用いた高分子の研究における尾崎教授ら47-49の戦略は、吸収分光法（遠赤外/テラヘルツ）とラマン散乱、さらに量子化学計算を合わせ用いるということである47-49。高分子の量子化学計算を行うときに問題となるのは、分子量の大きい試料をいかに扱うか、分子間、分子内相互作用をいかに計算に取り込むかということである。そのために山本ら47-49 は、Bouřら50によって提案された分子断片化 (Cartesian coordinte tensor transfer; CCT) 法を用いた。この方法はすでにペプチドやタンパク質の赤外、ラマン、ROA (Raman Optical Activity), VCD (Vibrational Circular Dichroism)のスペクトルの計算などでかなりの実績があった。分子断片化法では、高分子から数ユニットからなる断片を作り出し（fragment）、その断片について部分的に構造最適化し、さらに各々の断片の特性テンソル（力場、赤外、ラマン強度と振動数のテンソルなど）をDFT計算する50。得られたテンソルは分子全体のスペクトルを計算するために元の鎖に転写される。この方法を用いて分子鎖間の相互作用のexplicitな計算が可能になる。計算モデルの作り方や計算方法の詳細については文献47を参照のこと。山本と佐藤らは、低波数分光法と量子化学計算を用いてpoly-(R)-3-hydroxybutyrate (PHB)47, poly(glycolic acid) (PGA) 48, nylon 649などいろいろな高分子の研究を行った。

本HP「遠赤外/テラヘルツ/低波数ラマン分光法」において遠赤外分光法と量子化学計算法によるNylon 6 のバンドの帰属と構造、物性の研究について紹介した。

量子化学のラマン分光法への応用は赤外分光法への応用より少し遅れたが、やはり1990年代半ばごろから、次第に活発になった。今日ではラマン光学活性 (ROA; Raman Optical Activity)51,52や表面増強ラマン散乱 (Surface-enhanced Raman Scattering; SERS) 53,54 の研究へも量子化学計算が用いられている。ここでは山本ら55によるROAと量子化学計算によるPoly-L-alanineの溶媒和の研究について解説する。

ROAは溶液中のポリペプチドやタンパク質の2次構造を調べるのにきわめて有効な手法である51,52。山本ら55は最も簡単なα―ヘリックスモデルであるにもかかわらず、十分にはROAスペクトルの解析が進んでいないpoly-L-alanine (PLA) を研究テーマに選んだ。PLAはdichloroacetic acid (DCA) のように強い極性の有機溶媒中ではα―ヘリックス構造を取ることが知られている。図18はペプチドの溶媒和構造 (hydrated, αo)と非溶媒和構造 (non-hydrated, αc)　の断片を示す55。これらの構造のねじれ角（φi+1,ψi）は、それぞれ (-66°, -41°), (-59°, -44°) である。ねじれ角の差は小さく、通常の方法でこの差を見分けることは難しく、ROAが非常に有効である。ROAスペクトルの中でもとくに拡張アミドIII領域 (1400-1300 cm-1, CHとNHの変角振動がカップルしたモードによるバンドが観測される) は、溶媒和したα―ヘリックス構造を調べるのに有用である。タンパク質やポリペプチドの拡張アミドIII領域には正のピークが1340 cm-1 (type Iバンド)と1300 cm-1 (type IIバンド) に観測される。前者のバンドを与えるのは、親水性環境にあるα―ヘリックス構造で、そのamide基は溶媒分子あるいは極性の側鎖と水素結合している　（図18、hydrated, α0コンフォメーション）。一方、後者のバンドを与えるα―ヘリックス構造は疎水性の環境にあるもので、外部への水素結合はない状態である（図18、unhydrated, αcコンフォメーション）。これまではこれら2本のROAバンドの強度比は、αcとαoのコンフォメーションの存在比のマーカーであると示唆されてきた56。しかしながら山本ら55が行った基準モードの最適化と分子断片化法を組み合わせたROAスペクトルの計算シミュレーションによると、溶媒の誘電率の変化が強度比の変化の主たる原因で、コンフォメーション変化の影響はマイナーなものであることが分かった。

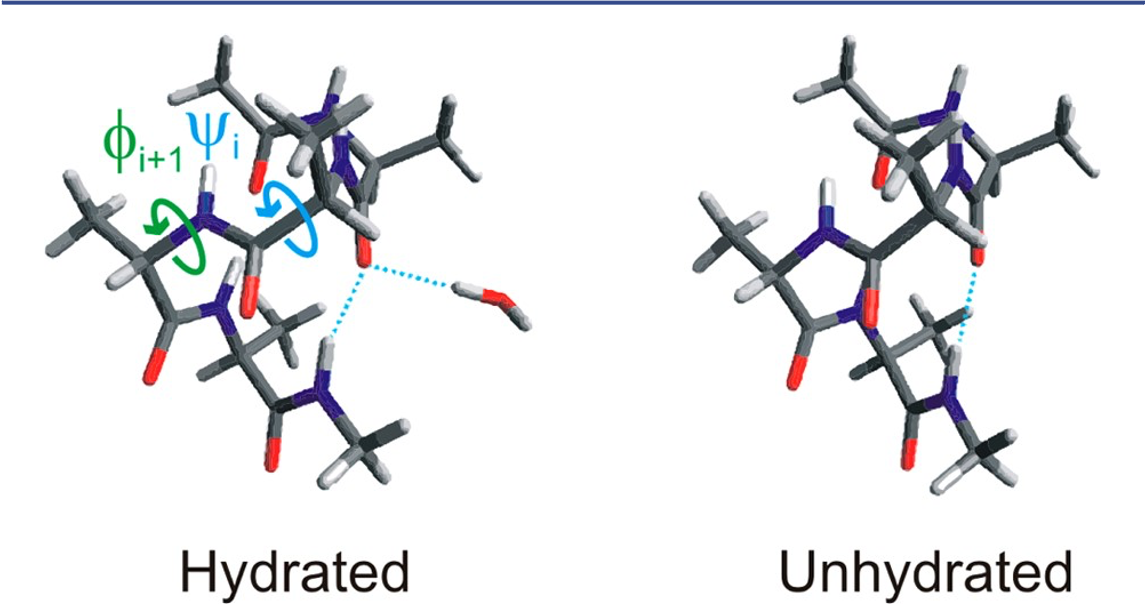
図18 ペプチドの溶媒和構造 (hydrated,αo)と非溶媒和構造 (non-hydrated,αc)の断片55。

山本ら55のシミュレーションでは、溶媒はconductor-like continuum solvent model (CPCM)を用いてモデル化された。計算のための初期構造はAc-(Ala)18-NHMeで、ペプチドの2面角は、溶媒和したα－ヘリックス構造に対しては、(-66°, -41°)、溶媒和していないα―ヘリックス構造に対しては、(-59°, -44°) が与えられた。計算には分子断片化法を用いている。通常はB3LYP/6-311++G** levelが用いられたが、他の関数、base sets,いろいろな溶媒モデル(CPCM)も用いている。

図19 PLAのDCAとCHCl3/DCA=7/3(v/v) 溶液のROAスペクトル56。

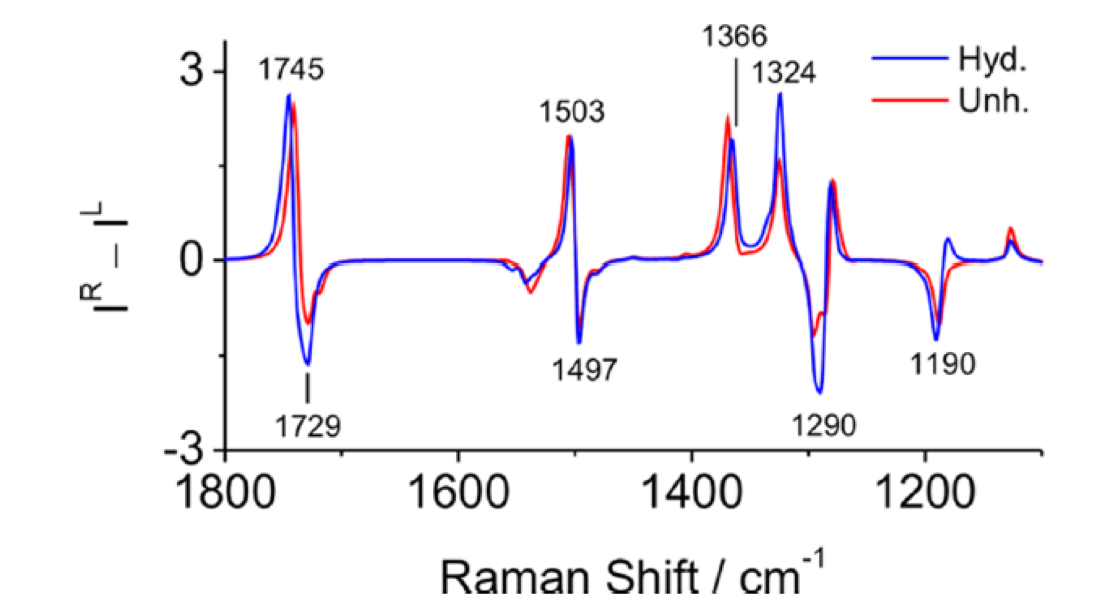
図20 B3LYP/6-311++G**levelで計算した溶媒和した(Ala)18と溶媒和していない(Ala)18の計算ROAのスペクトル55

図19はPLAのDCAとCHCl3/DCA=7/3(v/v) 溶液のROAスペクトルである56。一方、図20はB3LYP/6-311++G**levelで計算した溶媒和した(Ala)18と溶媒和していない(Ala)18の計算ROAのスペクトルである55。実験ROAスペクトルの1338, 1304, 1278 cm-1 の +/+/- の3本のピークは、計算ROAスペクトルではそれぞれ1366, 1324, 1290 cm-1に確認された。計算スペクトルにおける1366 (type I)と1324 (type II) cm-1のバンドは、いずれもCα-H変角振動によるバンドで、それらの振動では水素原子がそれぞれおおよそCα-Nあるいは Cα-C(=O)結合に沿って角度を曲げる。溶媒和構造のスペクトルの計算ではtype I バンドの強度がtype II バンドの強度のそれよりも弱い。一方、溶媒和していない構造のスペクトルでは、type I バンドの方がtype IIバンドより強い。実験スペクトルにおけるtype I とtype II のスペクトルの相対強度 (II/III) は、DCA溶媒では1.26, CHCl3/DCA=7/3(v/v) 混合溶媒では、1.05であった（図19）。一方、溶媒和構造と非溶媒和構造に対する計算値はそれぞれ0.72と1.43であった（図20）。すなわち、計算結果は溶媒和構造と非溶媒和構造の平衡が溶媒の極性で変化するという以前の実験結果の解釈とは合わない結果となった。以下に示すように、山本ら55の量子化学計算に基づく研究結果は、2本のバンドの強度比 (II/III) を決める重要な要素はペプチドの構造変化ではなく、周りの溶媒の誘電率であることを示唆した。

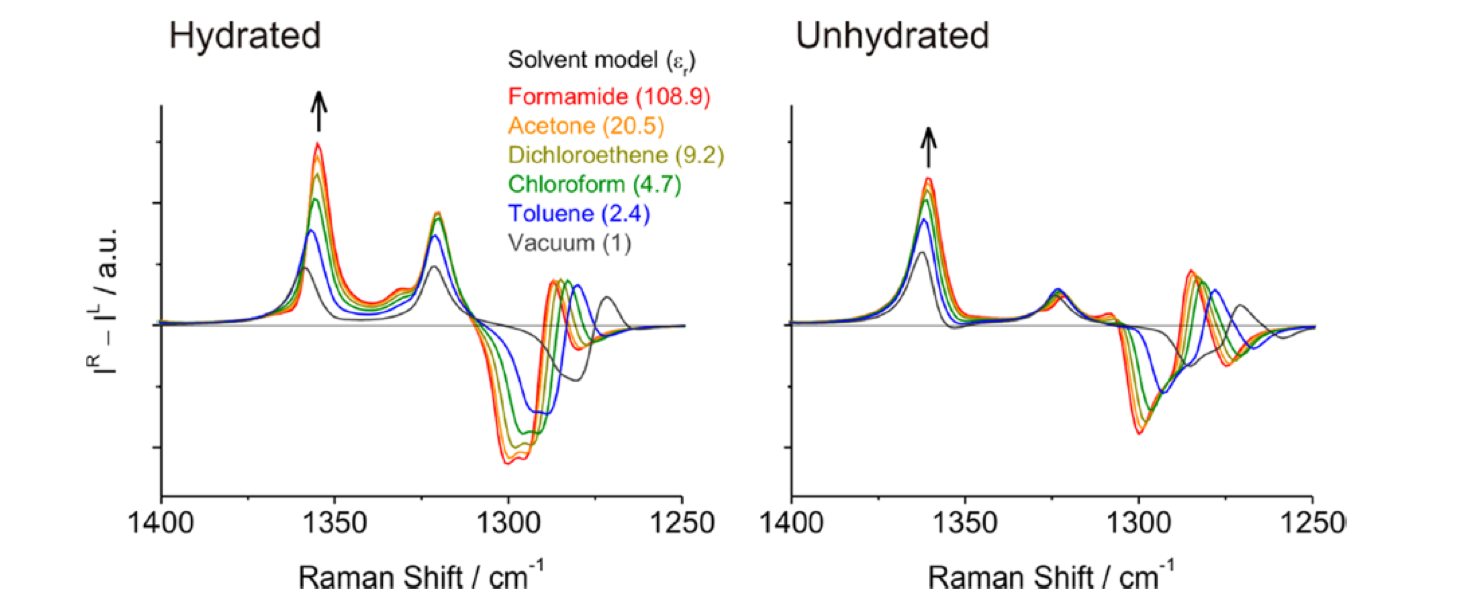
図21 拡張アミドIII領域における計算ROAスペクトルの誘電率依存性60。

図21は拡張アミドIII領域における計算ROAスペクトルの誘電率依存性である55。溶媒和したα―ヘリックス構造に対しては1360 cm-1バンド(type I)は、誘電率が増大するとともに強度が強くなり、低波数側にシフトした。しかし1320 cm-1のバンド(type II)の強度と振動数はほとんど変化しない。誘電率が最も大きいformamideのII/III はvaccumの場合に比べて1.5倍である。このように、拡張アミドIII領域は誘電率に非常に敏感に変化する。非溶媒和構造に対してはII/III は約4である（図21右）。図22は計算で求めた相対強度 (II/III) と溶媒の誘電率の関係を示したものである55。この図には実験結果も含めてある。非溶媒和構造に対する計算値は実験値よりも約４倍大きい、しかし溶媒和構造に対する計算値は実験値に非常に近い。この図の結果は、与えられた実験条件のものとでは、非溶媒和α―ヘリックス構造はマイナーなコンフォメーションであることを示す。したがって実験で得られた強度比は、溶媒和α―ヘリックス構造についての誘電率の変化で説明することができ、構造変化とは関係がないことが明らかになった55。

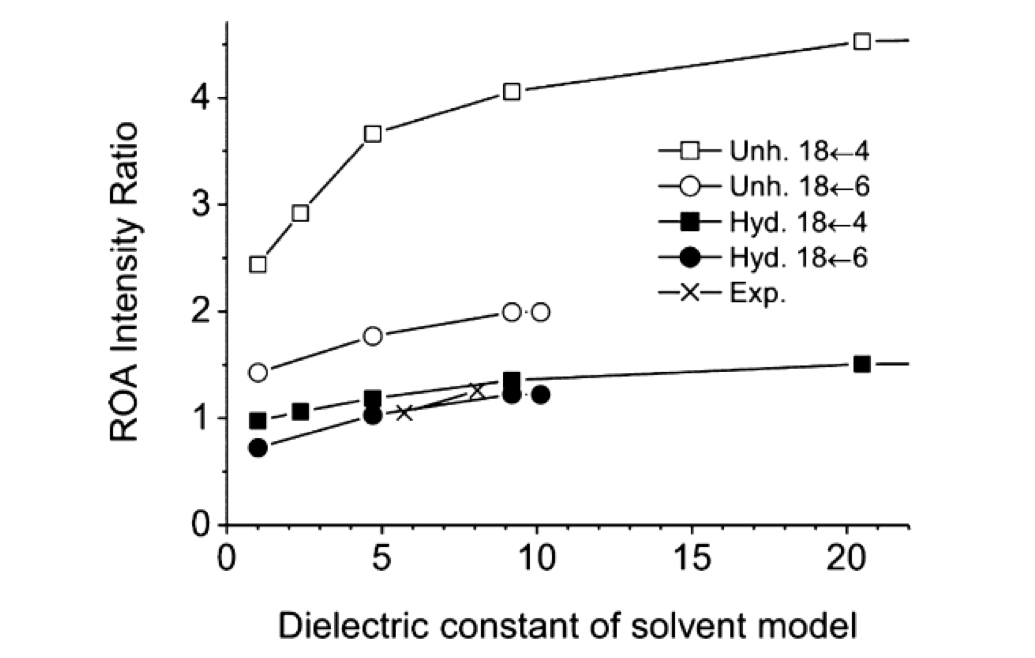
図22 計算で求めた相対強度 (II/III) と溶媒の誘電率の関係55。

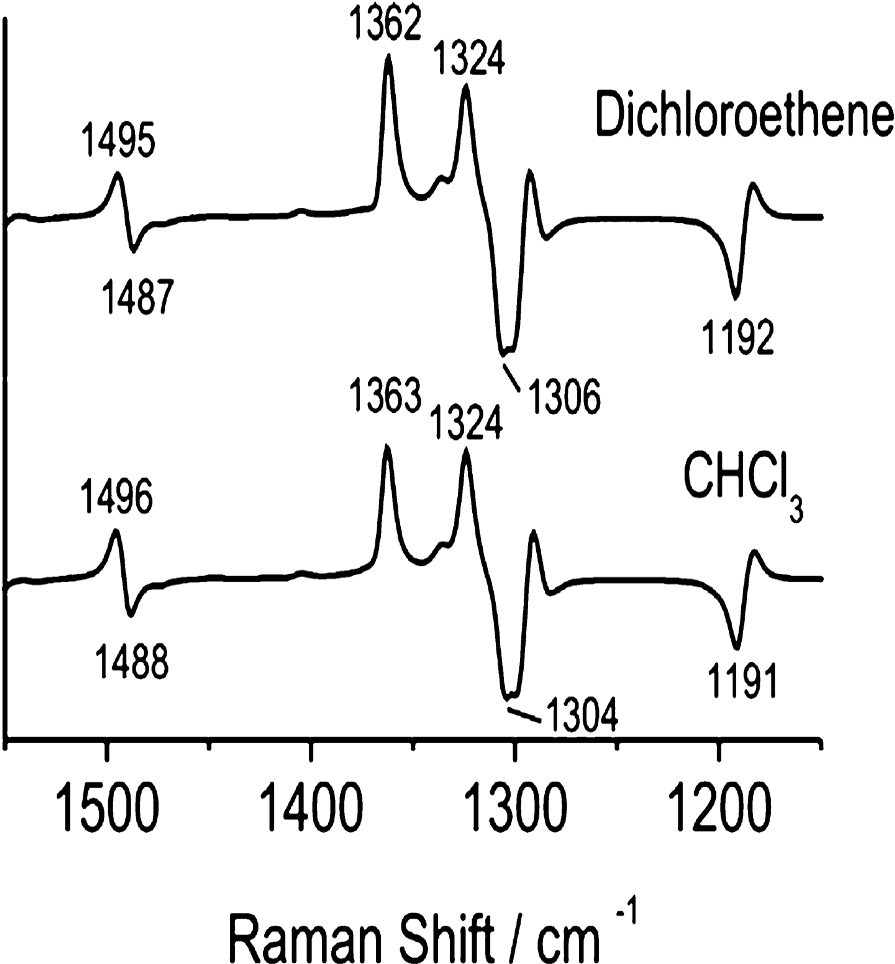
図23 溶媒和構造のPLAのシミュレーションスペクトル55。

図23は溶媒和構造のPLAのシミュレーションスペクトルである60。ここでは、dichloroethane (εr=9.2) とCHCl3 (4.7)のCPCMモデルが、DCA(8.1), CHCl3/DCA=7/3(v/v) (5.7)の実験溶媒をまねるのに用いられた。Type I とtype IIの強度比のわずかな変化が見事に計算で再現されている。以上の実験スペクトルと計算スペクトルの類似から山本ら55は、PLAは溶媒和構造のみを取っていると結論した。彼らの研究は、ROAのバンドがα―ヘリックスの近傍の溶媒の極性を見分ける能力があるので、タンパク質のフォールディングのプロセス、とくに溶媒和したα―ヘリックス構造の変化を含むフォールディングの解明に有力であることを示した55。

1. a) Ozaki, Y. Bull. Chem. Soc. Jpn, 2019, 92, 629-654. b) 尾崎幸洋、分光研究 2019, 68, 81-116.

2. 濵口宏夫、岩田耕一、ラマン分光学；講談社：東京、2015.

3. 分光研究、2019年, Vol. 68, No.1-6.ラマン分光特集号.

4．古川行夫、赤外分光学；講談社：東京、2018.

5. Ozaki, Y.; Huck, C. W.; Tuchikawa, S.; Engelsen, S. B. eds.; Near-infrared Spectroscopy; Theory, Spectral Analysis, Instrumentation, and Applications, Springer, 2020.

6. a) Czarnecki, M. A.; Morisawa, Y.; Futami, Y.; Ozaki, Y. Chem. Rev., 2015, 115, 9707-9744.b) 尾崎幸洋、近赤外分光学；講談社：東京、2015.

7. a) Peiponen, K. E.; Zeitler, J. A.; Kuwata-Gonokami, M. eds.; Terahertz Spectroscopy and Imaging, Springer, 2013. b) Coutaz, J.-L.; Garet, F.; Wallace, V. P. Terahertz Spectroscopy: An Introductory Textbook, Pan Stanford, 2018.

8. 分光研究　2005年、Vol. 54, No.1-6.テラヘルツ・遠赤外分光特集号

9. Wojcik, M. J.; Nakatsuji, H.; Kirtman, B.; Ozaki, Y., Eds.; Frontiers of Quantum Chemistry, Springer Nature, Singapore, 2018.

10. Ozaki, Y.; Wojcik, M. J.; Popp, J.; Molecular Spectroscopy; A Quantum Chemical Approach, Wiley-VCH, Weinheim, Germany, 2019.

11. Yoshida, H. Takeda, K.; Okamura, J.; Ehara, A.; Matsuura, H. J. Phys. Chem. A, 2002, 106, 3580-3586.

12. Bowman, J. M. J. Chem. Phys. 1978, 68, 608-610.

13. a) Yagi, K.; Keceli, M.; Hirata, S. J. Chem. Phys. 2012, 137, 204118. b) 八木清、分光研究、2012, 61, 163-168.

14. Tanaka, T.; Nakajima, A.; Watanabe, A.; Ohno, T.; Ozaki, Y.; Vib. Spectrosc., 2004, 34, 157-167.

15. Katsumoto, Y.; Tanaka, T.; Ozaki, Y.; J. Phys. Chem., 2005, 109, 20690-20696.

16. Ozaki, Y.; Kawata, S. Eds., Far- and Deep-Ultraviolet Spectroscopy, Springer, Tokyo, 2015.

17. a) Ozaki, Y.; Morisawa, Y.; Ikehata, A.; Higashi, N. Appl. Spectrosc., 2012, 66, 1-24.
b) Morisawa, Y.; Tanabe, I.; Ozaki, Y. In Frontiers and Advances in Molecular Spectroscopy, Laane, J. Ed., Elsevier, Amsterdam, 2018; pp. 251-286. c) Tanabe, I. Ozaki, Y. J. Mater. Chem. C. 2016, 4, 7706-7717.

18. 東昇、池羽田晶文、尾崎幸洋、分光研究 2008, 57, 2-11.

19. a) 森澤勇介, 分光研究 2016, 65, 91-103. b) 田邉一郎、応用物理2019, 88, 646-652.

20. Morisawa, Y.; Ikehata, A.; Higashi, N.; Ozaki, Y. J. Phys. Chem. A. 2011, 115, 562-568.

21. Morisawa, Y.; Tachibana, S.; Ehara, M.; Ozaki, Y. J. Phys. Chem., 2012, 116, 11957-11964.

22. Morisawa, Y.; Yasunaga, M.; Fukuda, R.; Ehara, M.; Ozaki, Y. J. Chem. Phys., 2013, 139, 154301.

23. Ehara, M.; Morisawa, Y. In Molecular Spectroscopy; A Quantum Chemical Approach, Ozaki, Y.; Wojcik, M. J.; Popp, J. Eds.; Wiley-VCH, Weinheim, Germany, 2019; pp119-146.

24. Morisawa, Y.; Yasunaga, Sato, H.; Fukuda, R.; Ehara, M.; Ozaki, Y. J. Phys. Chem. B, 2014, 118, 11855-11861.

25. Morisawa, Y.; Tachibana, S.; Ikehata, A.; Yang, T.; Ehara, M.; Ozaki, Y. ACS Omega, 2017, 2, 618-625.

26. a) Tanabe, I.; Suyama, A.; Sato, T.; Fukui K. Analyst, 2018, 143, 2539-2545. b) Tanabe, I.; Suyama, A.; Sato, T.; Fukui K. Anal. Chem., 2019, 91, 3436-3442.

27. Beć, K. B.; Morisawa, Y.; Kobashi, K.; Grabska, J.; Tanabe, I.; Ozaki, Y. J. Phys. Chem. C, 122, 28998-29008.

28. Beć, K. B.; Morisawa, Y.; Kobashi, K.; Grabska, J.; Tanabe, I.; Tanimura, E.; Sato, H.; Wójcik, M. J.; Ozaki, Y. Phys. Chem. Chem. Phys., 2018, 20, 8859-8873.

29. Yagi, K. In Molecular Spectroscopy; A Quantum Chemical Approach, Ozaki, Y.; Wojcik, M. J.; Popp, J. Eds.; Wiley-VCH, Weinheim, Germany, 2019; pp147-170.

30. Beć, K. B.; Grabska, J.; Huck, C. W. Ozaki, Y. In Molecular Spectroscopy; A Quantum Chemical Approach, Ozaki, Y.; Wojcik, M. J.; Popp, J. Eds.; Wiley-VCH, Weinheim, Germany, 2019; pp353-388.

31. Jung, J. O. Gerber, R. B. J. Chem. Phys. 1996, 105, 10332-10348.

32. Clabo, D. A.; Allen, W. D.; Remington, R. B.; Yamaguchi, Y.; Schaefer III, H. F. Chem. Phys. 1988, 123, 187-239.

33. Beć, K. B.; Grabska, J.; Ozaki, Y.; Hawranek, J. P.; Huck, C. W. J. Phys. Chem. A, 2017, 121, 1412-1424.

34. Beć, K. B.; Grabska, J.; Czarnecki, M. A.; Huck, C. W.; Wojcik, M. J.; Nakajima, T.; Ozaki, Y. J. Phys. Chem. B, 2019, 123, 10001-10013.

35. Barone, V. J. Chem. Phys. 2005, 122, 14108-14118.

36. Peng, C. S.; Jones, K. C.; Tokmakoff, A. J. Am. Chem. Soc. 2011, 133, 15650–15660.

37. a) Krummel, A. T.; Zanni, M. T. J. Phys. Chem. B, 2006, 110, 13991-14000. b) Krummel, A. T.; Mukherjee, P.; Zanni, M. T. J. Phys. Chem. B 2003, 107, 9165-9169.

38. Beć, K. B.; Futami, Y.; Wójcik, M. J.; Ozaki, Y. Phys. Chem. Chem. Phys. 2016, 18, 13666.

39. Beć, K. B.; Futami, Y.; Wójcik, M. J.; Nakajima, T.; Ozaki, Y. J. Phys. Chem. A, 2016, 120, 6170.

40. Grabska, J.; Beć, K. B.; Ishigaki, M.; Huck, C. W.; Ozaki, Y. J. Phys. Chem. B, 2018, 122, 6931.

41. Kirchler, C. G.; Pezzei, C. K.; Beć, K. B.; Mayr, S.; Ishigaki, M.; Ozaki, Y.; Huck, C. W. Analyst, 2017, 142, 455-464.

42. Futami, Y.; Ozaki, Y.; Hamada, Y.; Wójcik, M. J.; Ozaki, Y. Chem. Phys. Lett. 2009, 482, 320-324.

43. Futami, Y.; Ozaki, Y.; Hamada, Y.; Wójcik, M. J.; Ozaki, Y. J. Phys. Chem. A, 2011, 115, 1194-1198.

44. Gonjo, T.; Futami, Y.; Morisawa, Y.; Wójcik, M. J.; Ozaki, Y. J. Phys. Chem. A, 2011, 115, 9845-9853.

45. Schuler, M. J.; Hofer, T. S.; Morisawa, Futami, Y.; Huck, C. W.; Ozaki, Y, submitted for publication.

46. Beć, K. B.; Karczmit, D.; Kwasniewicz, M.; Ozaki, Y.; Czarnecki, M. A. J. Phys. Chem. B, 2019, 123, 20, 4431-4442.

47. Yamamoto, S.; Morisawa, Y.; Sato, H.; Hoshina, H.; Ozaki, Y. J. Phys. Chem. B, 2013, 117, 2180-2187.

48. Yamamoto, S.; Miyada, M.; Y.; Sato, H.; Hoshina, H.; Ozaki, Y. J. Phys. Chem. B, 2017, 121, 1128-1138.

49. Yamamoto, S.; Onishi, E.; Sato, H.; Hoshina, H.; Ishikawa, D.; Y. Ozaki, J. Phys. Chem. B, 2019, 123, 5368-5376.

50. a) Bouř, P.; Sopková, J.; Bednárová, L.; Maloň, P.; Keiderling, T. A. J. Comput. Chem. 1997, 18, 646−659. b) Yamamoto, S.; Li, X.; Ruud, K.; Bouř, P. J. Chem. Theory Comput. 2012, 8, 977-985.

51. Bouř, P.; Keidering, T. A. J. Chem. Phys. 2002, 117, 4126-4132.

52. Yamamoto, S.; Bouř, P.; In Frontiers of Quantum Chemistry, Wojcik, M. J.; Nakatsuji, H.; Kirtman, B.; Ozaki, Y., Eds.; Springer Nature, Singapore, 2018. pp181-197.

53. Wu, D.-Y.; Chen, Y.-L.; Wu, Y.-F.; Tian, Z.-Q. In Molecular Spectroscopy; A Quantum Chemical Approach, Ozaki, Y.; Wojcik, M. J.; Popp, J. Eds.; Wiley-VCH, Weinheim, Germany, 2019; pp537-574.

54. Mueller, C. M.; Gieseking, R. L. M.; Schatz, G. C. In Molecular Spectroscopy; A Quantum Chemical Approach, Ozaki, Y.; Wojcik, M. J.; Popp, J. Eds.; Wiley-VCH, Weinheim, Germany, 2019; pp575-596.

55. Yamamoto, S.; Furukawa, T.; Bouř, P.; Ozaki, Y. J. Phys. Chem. A, 2014, 118, 3655-3662.

56. McColl, I. H.; Blanch, E. W.; Hecht, L.; Barron, L. D. J. Phys. Chem. A, 2004, 126, 8181-8188.